View the full abstracts of the ADJOINT 2020 Research Topics below.
- Tepper Gill (Howard University): Analysis, PDEs, and Mathematical Physics
- Abba Gumel (Arizona State University): Mathematics of Malaria Transmission Dynamics
- Ryan Hynd (University of Pennsylvania): Hamilton-Jacobi Equations in High Dimensions
- Bonita V. Saunders (National Institute of Standards and Technology): Validated Numerical Computations of Mathematical Functions
- Craig Sutton (Dartmouth College): Explorations in Inverse Spectral Geometry
Tepper Gill (Howard University)
Analysis, PDEs, and Mathematical Physics
The center of mass for this research is a new class of separable Banach spaces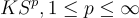 
, which contains each corresponding 
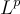space as a dense continuous embedding. These spaces are interesting because they contain the HK-integrable functions and the space of distributions. The HK- integral is easy to understand, extends the Lebesgue integral and integrates non-absolutely integrable functions. The spaces generate an arena for a number of interesting research topics in analysis, partial differential equations and mathematical physics.
Abba Gumel (Arizona State University)
Mathematics of the Transmission Dynamics and Control of the 2019 Novel Coronavirus
The world is currently facing a devastating pandemic of a novel Coronavirus (COVID-19), which started as an outbreak of pneumonia of unknown cause in Wuhan, China in December of 2019. As of April 26, 2020, COVID-19 (caused by the novel SARS-CoV-2 coronavirus) has spread to over 210 countries and territories, causing about three million infections and 207,000 deaths. In the absence of a safe and effective vaccine against COVID-19, and safe and approved antivirals, control and mitigation efforts are focused on the use of non-pharmaceutical interventions, such as social-distancing, quarantine, aggressive containment (i.e., rapid detection, isolation and contact-tracing of confirmed cases), use of face masks in public, etc.
The purpose of this project is to use mathematical modeling approaches and rigorous analysis, coupled with data analytics, to assess the population-level impact of various non-pharmaceutical interventions on the control and mitigating the burden of the pandemic. In particular, the models to be developed will take the form of deterministic (autonomous and non-autonomous) systems of nonlinear differential equations. The project entails the rigorous analysis of the models (using theories and techniques from nonlinear dynamical systems, particularly bifurcation theory) to gain insight into their dynamical features and to obtain epidemiological thresholds, in parameter space, that govern the persistence or effective control (elimination) of the pandemic. Furthermore, statistical tools will be used to estimate the parameters of the models, as well as to fit the models with available data and to carry out uncertainty and sensitivity analyses.
The ultimate goal of the project is to contribute, through mathematical modeling, rigorous analysis and statistical data analytics, to the development of effective public health policy for combating the pandemic in the U.S.
Ryan Hynd (University of Pennsylvania)
Hamilton-Jacobi Equations in High Dimensions
Hamilton-Jacobi equations (HJE) are partial differential equations which were first derived to study problems in classical mechanics. These equations have also played a central role in control and game theory. While these equations have been around for centuries, it was only in the 1980's that mathematicians first began to develop robust methods for studying solutions. Since then, there have been a plethora of interesting models that involve increasingly sophisticated HJE.
One direction of current interest is to study HJE when the dimension of the underlying space is large. This occurs, for example, in mechanics problems with a large number of particles, in control theory studies involving many possible states, and in differential games which include a large number of players. In these settings we can obtain very general HJE, sometimes called "master equations, which involve derivatives in time, space, and the distribution of agents.
In this project, we will discuss ways of studying solutions to these high dimensional HJE and hopefully identify some specific research avenues. I have worked a bit on these types of equations in the past, and I will be participating in a long program at UCLA's Institute for Pure and Applied Mathematics on this topic right before the ADJOINT program. My goal is to learn about all of the most salient problems related to this topic so that I can have several specific ones to suggest when we meet.
I imagine that this project will involve elements of partial differential equations, real and functional analysis, optimization, metric geometry, and perhaps some optimal transport. You won't need to be an expert in any one of these areas, but it will help to have some familiarity. I also think that doing this research will be an opportunity to gain expertise in these topics.
Bonita V. Saunders (National Institute of Standards and Technology)
Validated Numerical Computations of Mathematical Functions
During the late 1930s, 40s and 50s accurate tables of function values were calculated by human ‘computers’ to facilitate the evaluation of functions by interpolation. In addition to logarithmic and trigonometric functions, these reference tables included values for gamma, Legendre, Jacobian, Bessel, Airy, and other high level or “special” functions important for applied and physical applications.
The advent of reliable computing machines, computer algebra systems, and computational packages diminished the need for such reference tables, but today’s researchers and software developers still need a way to confirm the accuracy of numerical codes that compute mathematical function values. Project participants will be introduced to the field of validated computations of special mathematical functions, which is the development of codes that compute certifiably accurate function values that can be used to test the accuracy of values produced by personal, commercial, or publicly available codes.
The level and depth of some activities may depend on the skills and interests of the participants, but everyone will receive a brief overview of the field, look at examples that motivate the research, and become familiar with key terminology such as precision, base, floating point arithmetic, and correct rounding. Participants will also receive a short introduction to error analysis and have the opportunity to examine the DLMF Standard Reference Tables on Demand web site where a lot of the research discussed is being implemented. The goal is to provide an introduction to validated computing that piques the participant’s interest and provides the first step toward learning more about the field.
Texts:
Cuyt, A. A. M. et al., Handbook of continued fractions for special functions, Springer, Dordrecht, 2008, ISBN 978-1-4020-6948-2, DOI 10.1007/978-1-4020-6949-9
Higham, N. J., Accuracy and stability of numerical algorithms, 2nd ed., SIAM, Philadelphia, PA, 2002, ISBN 0-89871-521-0, DOI 10.1137/1.9780898718027
Craig Sutton (Dartmouth College)
Explorations in Inverse Spectral Geometry
Inverse spectral geometry is the study of the relationship between the spectrum of a closed Riemannian manifold — i.e., the sequence of eigenvalue (counting multiplicities) of the associated Laplace-Beltrami operator — and its underlying geometry. Two manifolds are said to be isospectral if their spectra agree and a geometric property is said to be audible or spectrally determined if it is encoded in the spectrum. The spectrum is known to encode the dimension, volume and total scalar curvature of a manifold; however, the literature contains numerous examples which demonstrate the spectrum does not completely determine the geometry of the underlying space. Nevertheless, it is expected that certain natural classes of Riemannian manifolds are characterized by their spectra. For example, it is widely believed that the round 
-sphere is uniquely characterized by its spectrum; however, to date, this has only been proven for round spheres of dimension at most six.
Our research group will work on problems motivated by the following questions:
- To what extent is the length spectrum of a manifold encoded in its Laplace spectrum?
- Is the local geometry of a low-dimensional manifold encoded in its spectrum?
- How are the covering spectrum of a Riemann surface and its Laplace spectrum related?