-
Workshop A Celebration for Women in Mathematics (2024) - May 12 Initiative
Organizers: Ini Adinya (University of Ibadan), Nasrin Altafi (Queen's University), Maria-Grazia Ascenzi (University of California Los Angeles), Shanna Dobson (University of California, Riverside), Malena Espanol (Arizona State University), Eleonore Faber (Karl-Franzens-Universität Graz; University of Leeds), Anna Fino (Università di Torino), Adi Glucksam (Northwestern University), Eloísa Grifo (University of Nebraska), Céleste Hogan (Texas Tech University), Ellen Kirkman (Wake Forest University), Kuei-Nuan Lin (Pennsylvania State University), Liangbing Luo (Lehigh University), LEAD Ornella Mattei (San Francisco State University), Claudia Miller (Syracuse University), Julia Plavnik (Indiana University), Claudia Polini (University of Notre Dame), Hema Srinivasan (University of Missouri), Špela Špenko (Université Libre de Bruxelles) "May 12 Initiative" Annual Workshop
"May 12 Initiative" Annual WorkshopThe Simons Laufer Mathematical Sciences Institute (SLMath) celebrates the "May 12 Initiative" with a panel discussion and social event open to all on the topic "Being a Woman in Mathematics". This is a hybrid event taking place on Zoom and in person at SLMath. This event is free and open to worldwide participation - please register online for Zoom link & details.
Updated on Apr 23, 2024 09:42 AM PDT -
MAY-UP Mathematically Advancing Young Undergraduates Program (MAY-UP) 2024
Updated on Apr 26, 2024 08:45 AM PDT -
Summer Graduate School Séminaire de Mathématiques Supérieures 2024: Flows and Variational Methods in Riemannian and Complex Geometry: Classical and Modern Methods (Montréal, Canada)
Organizers: Vestislav Apostolov (Université du Québec à Montréal), Eleonora Di Nezza (Institut de Mathématiques de Jussieu), Pengfei Guan (McGill University), Spiro Karigiannis (University of Waterloo), Julien Keller (Université du Québec à Montréal), Alina Stancu (Concordia University), Valentino Tosatti (New York University, Courant Institute)
This school will present various developments in Riemannian and Kähler geometry around the notion of curvature seen as a tool to describe and understand the geometry of the objects. The school will give graduate students the opportunity to learn key ideas and techniques of the field, with an emphasis on solidifying foundations in view of potential future research. The first week will be centered around the question of the existence of Kähler metrics with special curvature properties and the famous Yau-Tian-Donaldson conjecture. The second week will focus on geometric flows in Riemannian and complex geometry.
Updated on Mar 18, 2024 02:15 PM PDT -
MSRI-UP MSRI-UP 2024: Mathematical Endocrinology
Organizers: Alexander Diaz-Lopez (Villanova University), Maria Mercedes Franco (Queensborough Community College (CUNY)), Rebecca Garcia (Colorado College), LEAD Candice Price (Smith College), Robin Wilson (Loyola Marymount University)The MSRI-UP summer program is designed to serve a diverse group of undergraduate students who would like to conduct research in the mathematical sciences.
In 2024, MSRI-UP will focus on Mathematical Endocrinology. The research program will be led by Dr. Erica J. Graham, Associate Professor in the Department of Mathematics at Bryn Mawr College.
Updated on Mar 07, 2024 11:11 AM PST -
Summer Graduate School Particle interactive systems: Analysis and computational methods (SLMath)
Organizers: LEAD Irene M. Gamba (University of Texas, Austin), Francois Golse (École Polytechnique), Qin Li (University of Wisconsin-Madison), Chiara Saffirio (Universität Basel)
This summer school will focus on the introductory notions related to the passage of Newtonian and quantum many-body dynamics to kinetic collisional models of Boltzmann flow models arising in statistical sciences in connection to model reductions when continuum macro dynamics arises; and their numerical schemes associated to transport of kinetic processes in classical and data driven mean field dynamics incorporating recent tools from computational kinetics and data science tools. There will be two sets of lectures: “From Newton to Boltzmann to Fluid dynamics”, and “Kinetic collisional theory in mean field regimes: analysis, discrete approximations, and applications”. Each lecture series will be accompanied by a collaboration session, led by the lecturer and teaching assistants. The purpose of the collaboration sessions is to encourage and strengthen higher-level thinking of the materials taught in the lectures and to direct further reading for interested students. Interactive learning activities will be conducted. For example, students will be given problem sets associated with the lectures and will work in small groups to discuss concepts and/or find solutions to assigned problems. The students will also be encouraged to give oral or poster presentations on their solutions or other materials relevant to the course.
Updated on Apr 10, 2024 02:59 PM PDT -
Summer Graduate School Special Geometric Structures and Analysis (St. Mary's College)
Organizers: Costante Bellettini (University College London), LEAD Eleonora Di Nezza (Institut de Mathématiques de Jussieu), Song Sun (University of California, Berkeley) a Calabi-Yau manifold
a Calabi-Yau manifoldThis summer school will serve as an introduction to the SLMath program "Special geometric structures and analysis". There will be two mini-courses: one in Geometric Measure theory and the other in Microlocal Analysis. The aim is to give the basic notions of two subjects also treated during the program.
Updated on Apr 05, 2024 09:40 PM PDT -
Summer Graduate School Introduction to Quantum-Safe Cryptography (IBM Zurich)
Organizers: Jonathan Bootle (IBM Zürich Research Laboratory), Luca De Feo (IBM Zürich Research Laboratory)
This two week summer school, jointly organized by SLMath with IBM Zurich, will introduce students to the mathematics and algorithms used in the design and analysis of quantum-safe cryptosystems. Each week will be dedicated to two of the four families of quantum-safe schemes.
Updated on Apr 16, 2024 03:42 PM PDT -
Summer Graduate School H-principle (Sendai, Japan)
Organizers: Emmy Murphy (Princeton University), Takashi Tsuboi (RIKEN Interdisciplinary Theoretical and Mathematical Sciences Program) The image of a large sphere isometrically embedded into a small space through a C^1 embedding. (Attributions: E. Bartzos, V. Borrelli, R. Denis, F. Lazarus, D. Rohmer, B. Thibert)
The image of a large sphere isometrically embedded into a small space through a C^1 embedding. (Attributions: E. Bartzos, V. Borrelli, R. Denis, F. Lazarus, D. Rohmer, B. Thibert)This two week summer school, jointly organized by SLMath with RIKEN, will introduce graduate students to the theory of h-principles. After building up the theory from basic smooth topology, we will focus on more recent developments of the theory, particularly applications to symplectic and contact geometry, fluid dynamics, and foliation theory.
h-principles in smooth topology (Emmy Murphy)
Riemannian geometry and applications to fluid dynamics (Dominik Inauen)
Contact and symplectic flexibility (Emmy Murphy)
Foliation theory and diffeomorphism groups (Takashi Tsuboi)Updated on Apr 17, 2024 10:55 AM PDT -
Summer Graduate School Stochastic Quantization (SLMath)
Organizers: Massimiliano Gubinelli (University of Oxford), Martina Hofmanova (Universität Bielefeld), LEAD Hao Shen (University of Wisconsin-Madison), Lorenzo Zambotti (Sorbonne Université)
This summer school will familiarize students with the basic problems of the mathematical theory of Euclidean quantum fields. The lectures will introduce some of its prominent models and analyze them via the so called “stochastic quantization” methods, involving recently developed stochastic and PDE techniques. This is an area which is highly interdisciplinary combining ideas ranging from the theory of partial differential equations, to stochastic analysis, to mathematical physics. Our goal is to bring together students who are perhaps familiar with some but not all of these subjects and teach them how to integrate these different tools to solve cutting-edge problems of Euclidean quantum field theory.
Updated on Apr 24, 2024 03:23 PM PDT -
Summer Graduate School Koszul Duality in the Local Langlands Program (St. Mary's College)
Organizers: Clifton Cunningham (University of Calgary), LEAD Sarah Dijols (University of Calgary)
This summer school provides the mathematical background to recognize Koszul duality in representation theory. The school is especially oriented toward applications in the local Langlands program, with an emphasis on real groups. As Koszul duality patterns have been initially observed in the context of Hecke algebras, our school will also introduce the students to Hecke algebras and their categorifications.
Updated on Apr 12, 2024 11:27 PM PDT -
Summer Graduate School Introduction to the Theory of Algebraic Curves (UC Berkeley)
Organizers: Izzet Coskun (University of Illinois, Chicago), Eric Larson (Brown University), LEAD Hannah Larson (University of California, Berkeley), Isabel Vogt (Brown University)
In the last few years, there have been extraordinary developments in many aspects of curve theory. Beginning with many examples in low genus, this summer school will introduce the participants to the background behind these developments in the following areas:
- moduli spaces of stable curves
- Brill–Noether theory
- the extrinsic geometry of the curves in projective space
We will also include an introduction to some open problems at the forefront of these active areas.
Updated on Apr 19, 2024 10:16 AM PDT -
Summer Graduate School Mathematics of General Relativity and Fluids (FORTH, Greece)
Organizers: LEAD Mihalis Dafermos (Princeton University), Grigorios Fournodavlos (University of Crete), Juhi Jang (University of Southern California), Igor Rodnianski (Princeton University) ALCF Visualization and Data Analytics Team; Adam Burrows and the Princeton Supernova Theory Group, Princeton University
ALCF Visualization and Data Analytics Team; Adam Burrows and the Princeton Supernova Theory Group, Princeton UniversityThis summer school will give an accessible introduction to the mathematical study of general relativity, a field which in the past has had barriers to entry due to its interdisciplinary nature, and whose study has been concentrated at specific institutions, to a wider audience of students studying at institutions throughout the U.S., Europe and Greece. Another goal of the summer school will be to demonstrate the common underlying mathematical themes in many problems which traditionally have been studied by separate research communities.
Updated on Mar 19, 2024 04:24 PM PDT -
Summer Graduate School Analysis of Partial Differential Equations (Okinawa Institute of Science and Technology)
Organizers: Ugur Abdulla (Okinawa Institute of Science and Technology), Gui-Qiang Chen (University of Oxford)This two week summer school, jointly organized by SLMath with OIST, will offer the following two mini-courses:
- Measure-theoretical analysis, divergence-measure fields, and nonlinear PDEs of divergence form
This course will present some recent developments in the theory of divergence-measure fields via measure-theoretic analysis and its applications to the analysis of nonlinear PDEs of conservative form – nonlinear conservation laws. - Perron’s method and Wiener-type criteria in the potential theory of elliptic and parabolic PDEs
This course will present some recent developments precisely characterizing the regularity of the point at ∞ for second order elliptic and parabolic PDEs and broadly extending the role of the Wiener test in classical analysis.
Updated on Apr 19, 2024 12:54 PM PDT - Measure-theoretical analysis, divergence-measure fields, and nonlinear PDEs of divergence form
-
Summer Graduate School Mathematical Spin Glass Theory (Courant, NY)
Organizers: Antonio Auffinger (Northwestern University), Wei-Kuo Chen (University of Minnesota), LEAD Eliran Subag (Weizmann Institute of Science)
While their original aim was to explain the strange behavior of certain magnetic alloys, the study of spin glass models has led to a far-reaching and beautiful physical theory whose techniques have been applied to a myriad of problems in theoretical computer science, statistics, optimization and biology. As many of the physical predictions can be formulated as purely mathematical questions, often extremely hard, about large random systems in high dimensions, in recent decades a new area of research has emerged in probability theory around these problems.
Mathematically, a mean-field spin glass model is a Gaussian process (random function) on the discrete hypercube or the sphere in high dimensions. A fundamental challenge in their analysis is, roughly speaking, to understand the size and structure of their super-level sets as the dimension tends to infinity, which are often studied through smooth objects like the free energy and Gibbs measure whose origin is in statistical physics. The aim of the summer school is to introduce students to landmark results on the latter while emphasizing the techniques and ideas that were developed to obtain them, as well as exposing the students to some recent research topics.
Updated on Apr 19, 2024 03:00 PM PDT -
Summer Graduate School Statistical Optimal Transport (St. Mary's College)
Organizers: LEAD Promit Ghosal (Brandeis University), Jonathan Niles-Weed (New York University, Courant Institute), Marcel Nutz (Columbia University)
This summer school offers an exceptional opportunity for participants to delve into the intricate realm of statistical optimal transport theory. This captivating field stands at the crossroads of multiple disciplines, drawing from a rich tapestry of mathematical insights from diverse subjects, including partial differential equations, stochastic analysis, convex geometry, statistics, and machine learning, crafting a vibrant and interdisciplinary landscape. The foremost objective of this summer school is to create a dynamic learning environment that unites students from diverse backgrounds such as PDE theory, probability, or optimal transport.
Updated on Mar 20, 2024 02:04 PM PDT -
Summer Graduate School Noncommutative Algebraic Geometry
Organizers: Pieter Belmans (University of Luxembourg), Lander Hermans (Universiteit Antwerp), Wendy Lowen (Universiteit Antwerpen), Arne Mertens (Universiteit Antwerp), Michel VAN DEN BERGH (Hasselt University), Špela Špenko (Université Libre de Bruxelles)Created on Apr 03, 2024 05:26 PM PDT -
Summer Graduate School Computer Assisted Proofs in Applied Mathematics (SLMath)
Organizers: LEAD Jonathan Jaquette (New Jersey Institute of Technology), Evelyn Sander (George Mason University)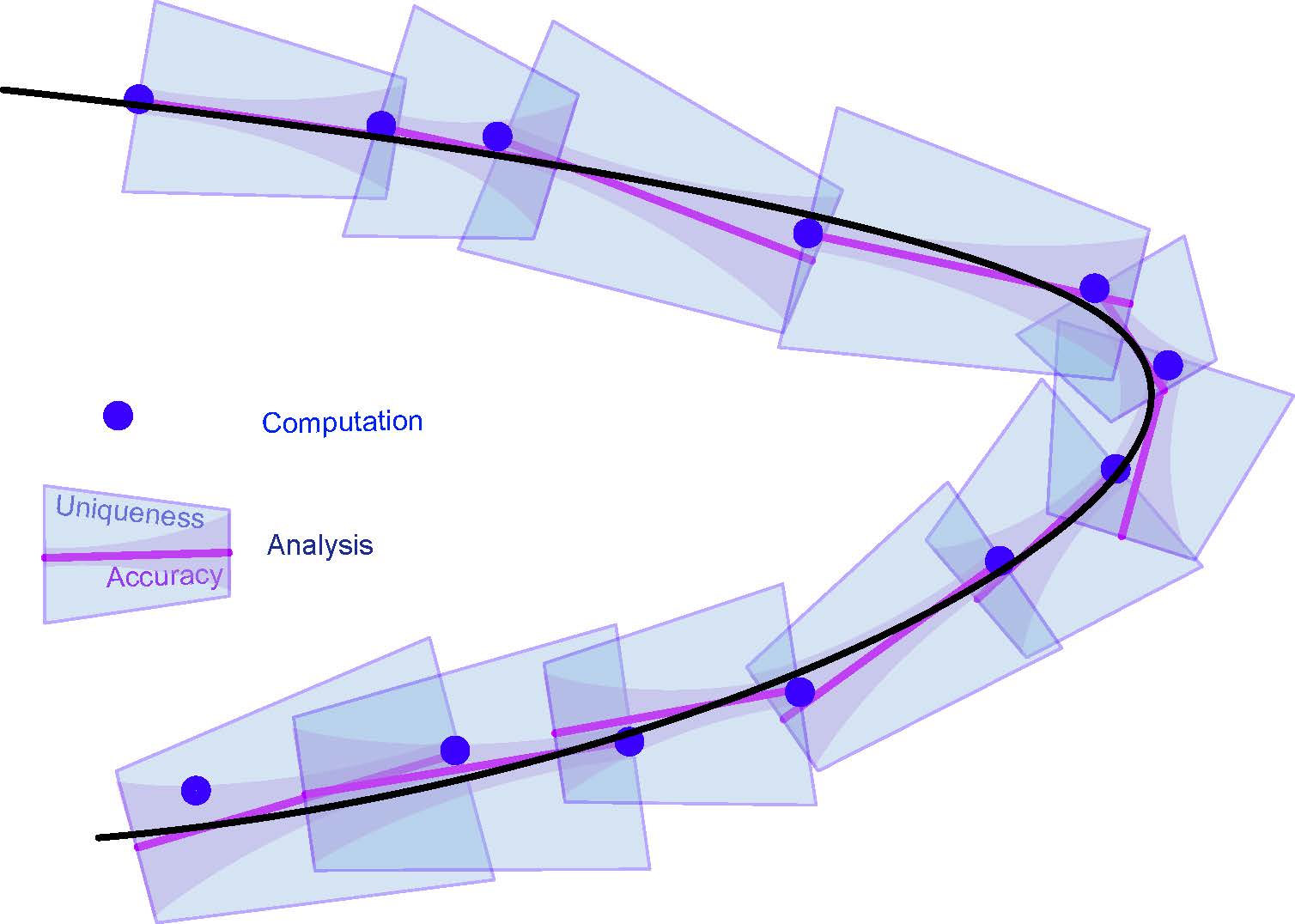
One of the core elements of applied mathematics is mathematical modeling consisting of nonlinear equations such as ODEs, and PDEs. A fundamental difficulty which arises is that most nonlinear models cannot be solved in closed form. Computer assisted proofs are at the forefront of modern mathematics and have led to many important recent mathematical advances. They provide a way of melding analytical techniques with numerical methods, in order to provide rigorous statements for mathematical models that could not be treated by either method alone. In this summer school, students will review standard computational and analytical techniques, learn to combine these techniques with more specialized methods of interval arithmetic, and apply these methods to establish rigorous results in otherwise intractable problems
Updated on Apr 08, 2024 08:55 AM PDT -
Summer Graduate School Geometry and Dynamics in Higher Rank Lie Groups (St. Mary's College)
Organizers: Richard Canary (University of Michigan), Sara Maloni (University of Virginia), Wenyu Pan (University of Toronto), Cagri Sert (University of Zurich), LEAD Tengren Zhang (National University of Singapore)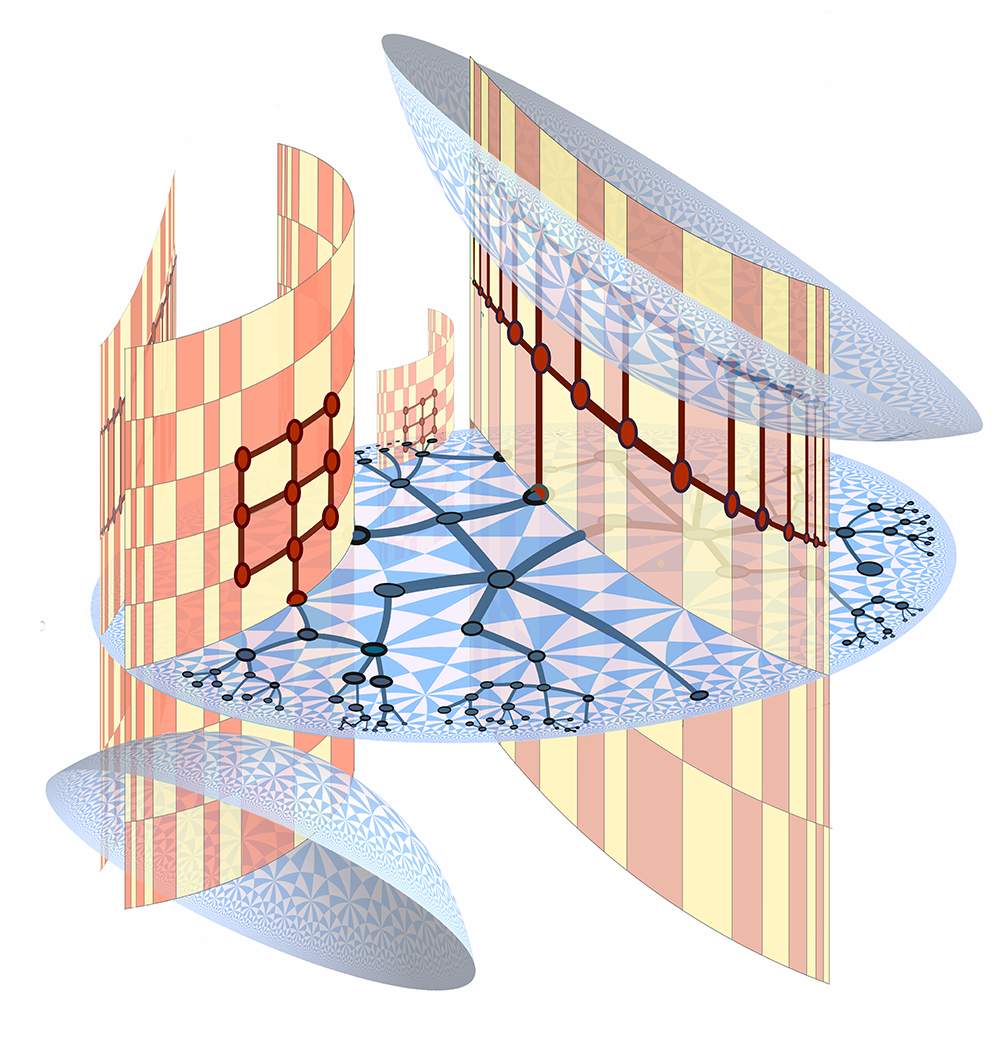 <p>Flats and hyperbolic planes in a higher rank symmetric space</p> Drawn by Steve Trettel.
<p>Flats and hyperbolic planes in a higher rank symmetric space</p> Drawn by Steve Trettel.Lie groups are central objects in modern mathematics; they arise as the automorphism groups of many homogeneous spaces, such as flag manifolds and Riemannian symmetric spaces. Often, one can construct manifolds locally modelled on these homogeneous spaces by taking quotients of their subsets by discrete subgroups of their automorphism groups. Studying such discrete subgroups of Lie groups is an active and growing area of mathematical research. The objective of this summer school is to introduce young researchers to a class of discrete subgroups of Lie groups, called Anosov subgroups.
Updated on Apr 18, 2024 08:43 AM PDT -
Summer Graduate School Topological and Geometric Structures in Low Dimensions (SLMath)
Organizers: LEAD Kenneth Bromberg (University of Utah), Kathryn Mann (Cornell University) <p>Laminations arise naturally in hyperbolic geometry and (pseudo-) Anosov flows [Image by Jeffrey Brock]</p>
<p>Laminations arise naturally in hyperbolic geometry and (pseudo-) Anosov flows [Image by Jeffrey Brock]</p>This school will serve as an introduction to the SLMath semester “Topological and Geometric Structures in Low-Dimensions”. The school consists of two mini-courses: one on Teichmüller Theory and Hyperbolic 3-Manifolds and the other on Anosov Flows on Geometric 3-Manifolds. Both topics lie at the interface of low-dimensional geometric topology (specifically, surfaces, foliations, and 3-manifolds) and low-dimensional dynamics. The first course will be targeted towards students who have completed the standard first year graduate courses in geometry, topology, and analysis while the second course will geared towards more advanced students who are closer to beginning research. However, we expect that all students will benefit from both courses.
Updated on Mar 21, 2024 09:48 AM PDT
|
|
Upcoming Educational Events |