-
Quantum Symmetries Reunion
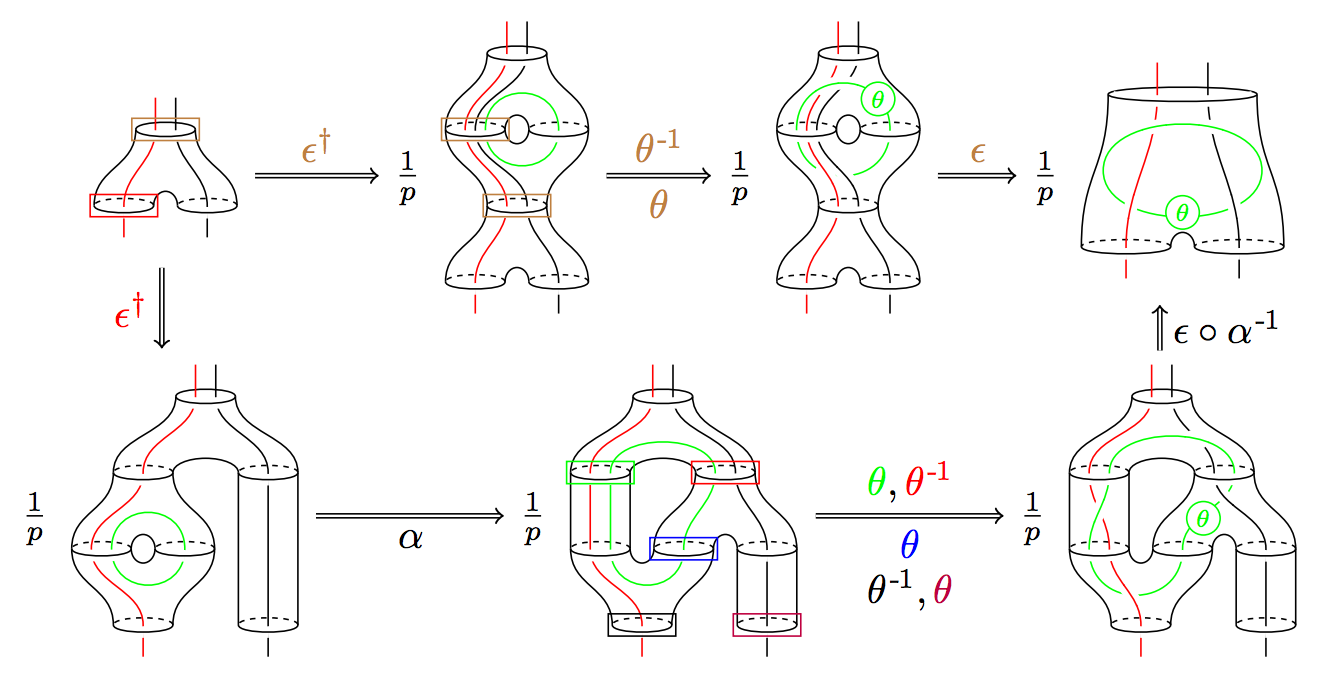 The study of tensor categories involves the interplay of representation theory, combinatorics, number theory, and low dimensional topology (from a string diagram calculation, describing the 3-dimensional bordism 2-category [arXiv:1411.0945]).
The study of tensor categories involves the interplay of representation theory, combinatorics, number theory, and low dimensional topology (from a string diagram calculation, describing the 3-dimensional bordism 2-category [arXiv:1411.0945]).Symmetry, as formalized by group theory, is ubiquitous across mathematics and science. Classical examples include point groups in crystallography, Noether's theorem relating differentiable symmetries and conserved quantities, and the classification of fundamental particles according to irreducible representations of the Poincaré group and the internal symmetry groups of the standard model. However, in some quantum settings, the notion of a group is no longer enough to capture all symmetries. Important motivating examples include Galois-like symmetries of von Neumann algebras, anyonic particles in condensed matter physics, and deformations of universal enveloping algebras. The language of tensor categories provides a unified framework to discuss these notions of quantum symmetry.
Updated on Sep 14, 2023 04:03 AM PDT -
New Frontiers in Curvature: Flows, General Relativity, Minimal Submanifolds, and Symmetry
Organizers: LEAD Ailana Fraser (University of British Columbia), Lan-Hsuan Huang (University of Connecticut), Richard Schoen (Stanford University), LEAD Catherine Searle (Wichita State University), Lu Wang (Yale University), Guofang Wei (University of California, Santa Barbara) Soap bubble: equilibrium solution of the mean curvature flow and constant curvature surface.
Soap bubble: equilibrium solution of the mean curvature flow and constant curvature surface.Geometry, PDE, and Relativity are subjects that have shown intriguing interactions in the past several decades, while simultaneously diverging, each with an ever growing number of branches. Recently, several major breakthroughs have been made in each of these fields using techniques and ideas from the others.
This program is aimed at connecting various branches of Geometry, PDE, and Relativity and at enhancing collaborations across these disciplines and will include four main topics: Geometric Flows, Geometric problems in Mathematical Relativity, Global Riemannian Geometry, and Minimal Submanifolds. Specifically the program focuses on a central goal, which is to advance our knowledge toward Riemannian (sub)manifolds under geometric conditions, such as curvature lower bounds, by developing techniques in, for example, geometric flows and minimal submanifolds and further fostering new connections.
Updated on Nov 17, 2022 10:10 AM PST -
Special Geometric Structures and Analysis
Organizers: Eleonora Di Nezza (Institut de Mathématiques de Jussieu), LEAD Mark Haskins (Duke University), Tristan Riviere (ETH Zurich), Song Sun (University of California, Berkeley), Xuwen Zhu (Northeastern University) “Plateau’s Memory ” (by A. van der Net): A soap film with singularities
“Plateau’s Memory ” (by A. van der Net): A soap film with singularitiesThis program sits at the intersection between differential geometry and analysis but also connects to several other adjacent mathematical fields and to theoretical physics. Differential geometry aims to answer questions about very regular geometric objects (smooth Riemannian manifolds) using the tools of differential calculus. A fundamental object is the curvature tensor of a Riemannian metric: an algebraically complicated object that involves 2nd partial derivatives of the metric. Many questions in differential geometry can therefore be translated into questions about the existence or properties of the solutions of systems of (often) nonlinear partial differential equations (PDEs). The PDE systems that arise in geometry have historically stimulated the development of powerful new analytic methods. In most cases the nonlinearity of these systems makes ‘closed form’ expressions for a solution impossible: instead more abstract methods must be employed.
Updated on Nov 10, 2022 04:20 PM PST -
Complementary Program 2024-25
The Complementary Program has a limited number of memberships that are open to mathematicians whose interests are not closely related to the core programs; special consideration is given to mathematicians who are partners of an invited member of a core program.
Updated on Nov 03, 2023 03:25 PM PDT -
Probability and Statistics of Discrete Structures
Organizers: Louigi Addario-Berry (McGill University), Christina Goldschmidt (University of Oxford), Po-Ling Loh (University of Cambridge), Gabor Lugosi (ICREA), Dana Randall (Georgia Institute of Technology), LEAD Remco van der Hofstad (Technische Universiteit Eindhoven) The minimum spanning tree of 100,000 uniformly random points. Colors encode graph distance from the root, which is red. Black points are those whose removal would disconnect at least 5% of the points from the rest.
The minimum spanning tree of 100,000 uniformly random points. Colors encode graph distance from the root, which is red. Black points are those whose removal would disconnect at least 5% of the points from the rest.This program is devoted to the study of the probabilistic and statistical properties of such networks. Central tools include graphon theory for dense graphs, local weak convergence for sparse graphs, and scaling limits for the critical behavior of graphs or stochastic processes on them. The program is aimed at pure and applied mathematicians interested in network problems.
Updated on Feb 29, 2024 02:57 PM PST -
Extremal Combinatorics
Organizers: LEAD David Conlon (California Institute of Technology), LEAD Jacob Fox (Stanford University), Penny Haxell (University of Waterloo), Janos Pach (Alfréd Rényi Institute of Mathematics), Maya Stein (Universidad de Chile), Andrew Suk (University of California, San Diego)
Extremal combinatorics concerns itself with problems about how large or small a finite collection of objects can be while satisfying certain conditions. Questions of this type arise naturally across mathematics, so this area has close connections and interactions with a broad array of other fields, including number theory, group theory, model theory, probability, statistical physics, optimization, and theoretical computer science.
Updated on Feb 29, 2024 02:56 PM PST -
Kinetic Theory: Novel Statistical, Stochastic and Analytical Methods
Organizers: Laurent Desvillettes (Université Paris Cité), Irene M. Gamba (University of Texas, Austin), Francois Golze (École Polytechnique), LEAD Pierre Emmanuel Jabin (Pennsylvania State University), Qin Li (University of Wisconsin-Madison), Chiara Saffirio (Universität Basel), Lexing Ying (Stanford University) Top: Neutrino interactions and neutrino-atom interactions. Bottom: Collision of two "waves"
Top: Neutrino interactions and neutrino-atom interactions. Bottom: Collision of two "waves"The focus of the proposed program is on so-called kinetic equations, describing the evolution of the of many-particle interacting systems. These models have the form of statistical flows, with their solutions being either a single or multiple point probability density functions or measures, supported in a space of attributes. The attributes are problem-dependent and can be molecular velocity, energy, opinion, wealth, and many others. The flow then predicts the evolution of the probability measure in time, position in space, and the interchanging of the particles' states by the transition probability.
The program will strive to give an overview of the novel mathematical tools used in kinetic theory through a broad range of classical and more recent applications.
Updated on Apr 17, 2024 08:58 AM PDT -
Recent Trends in Stochastic Partial Differential Equations
Organizers: Sandra Cerrai (University of Maryland), Yu Gu (University of Maryland), Massimiliano Gubinelli (University of Oxford), Davar Khoshnevisan (University of Utah), Andrea Nahmod (University of Massachusetts, Amherst), Hao Shen (University of Wisconsin-Madison), LEAD Lorenzo Zambotti (Sorbonne Université)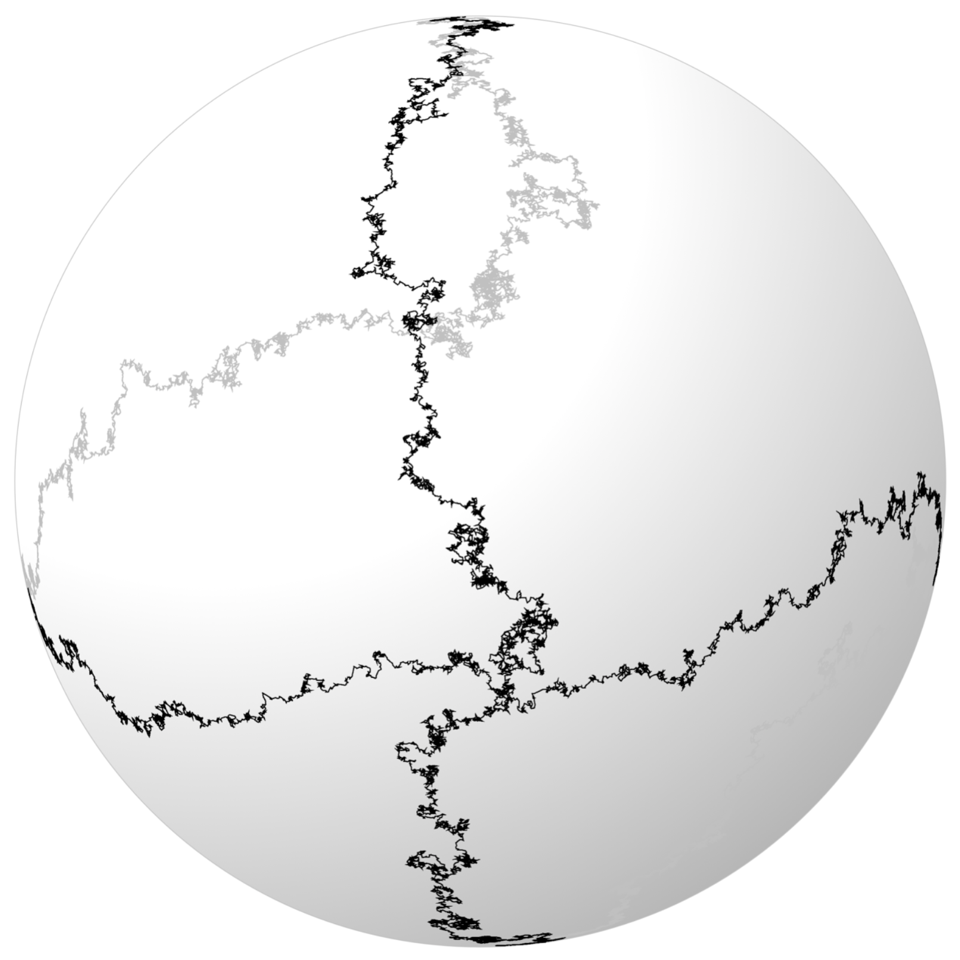 Solution to the geometric stochastic heat equation on the sphere at a fixed time
Solution to the geometric stochastic heat equation on the sphere at a fixed timeThe topic Singular Stochastic Partial Differential Equations (singular SPDE) has rapidly grown to be an active research area at the interface of Stochastic Analysis and PDEs on one hand, and Mathematical Physics on the other hand. During this decade we have witnessed a series of tremendous breakthroughs in the solution theories of SPDEs, universality problems, large-scale asymptotic behaviors of solutions, and foundational relations with quantum field theories and geometry. Many long-standing problems have been resolved via newly developed methods – notably the theories of regularity structures and paracontrolled distributions – and deep connections with other fields are quickly emerging.
It is a natural time to convene a large-scale semester program.
Updated on Apr 17, 2024 10:56 AM PDT -
Geometry and Dynamics for Discrete Subgroups of Higher Rank Lie Groups
Organizers: Martin Bridgeman (Boston College), LEAD Richard Canary (University of Michigan), Amir Mohammadi (University of California, San Diego), LEAD Hee Oh (Yale University), Maria Beatrice Pozzetti (Ruprecht-Karls-Universität Heidelberg), Jean-François Quint (CNRS - Université de Montpellier)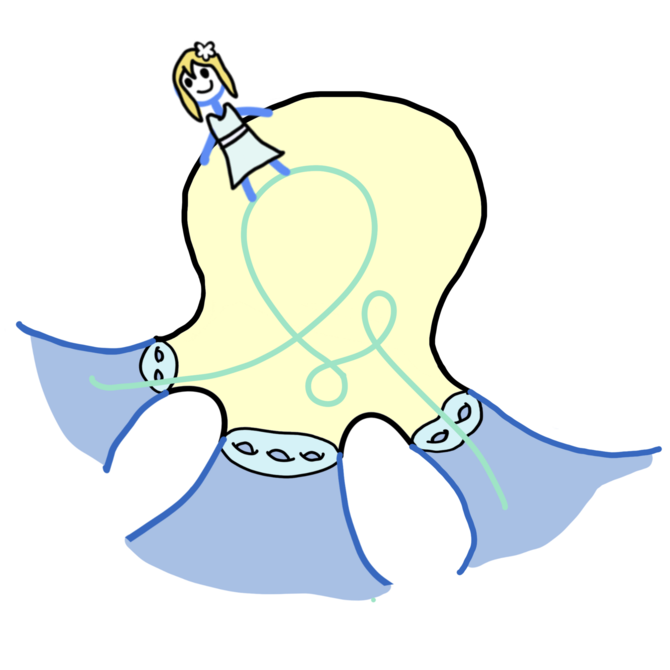 <p>This figure depicts dynamics of flows on convex cocompact hyperbolic 3-manifolds; where the girl is a traveller along a horocycle.</p>
<p>This figure depicts dynamics of flows on convex cocompact hyperbolic 3-manifolds; where the girl is a traveller along a horocycle.</p>This research program will bring together two intellectual communities that have made significant advances in the study of discrete subgroups of higher rank semisimple Lie groups: the homogeneous dynamics community and the community studying geometric structures and Anosov groups.
Updated on Apr 17, 2024 11:08 AM PDT -
Topological and Geometric Structures in Low Dimensions
Organizers: Ian Agol (University of California, Berkeley), Kenneth Bromberg (University of Utah), Sebastian Hensel (LMU München), Christopher Leininger (Rice University), Kathryn Mann (Cornell University), LEAD Yair Minsky (Yale University), Rachel Roberts (Washington University in St. Louis) The stable and unstable foliations near a singular orbit of a pseudo- Anosov flow in 3 dimensions. Courtesy Michael Landry.
The stable and unstable foliations near a singular orbit of a pseudo- Anosov flow in 3 dimensions. Courtesy Michael Landry.Low dimensional topology is a meeting place for many objects and ideas from diverse areas of mathematics, including foliation theory, geometry, and smooth and conformal dynamics. For instance, many foliations on 3-manifolds admit transverse flows, connecting (local) leafwise homeomorphisms to flow dynamics and the mapping class groups of the leaves. Leafwise conformal or hyperbolic structures can be approached through Teichmüller theory, and connect again to one-dimensional dynamics through "universal circles" organizing compactifications of all the leaves or of the flow space. Many of these ideas originate in work of Thurston but in recent years have diverged and are ripe for reconnection.
The program will bring together experts in all these fields together with younger researchers, who together can form new connections and open new areas for exploration.Updated on Apr 17, 2024 11:10 AM PDT -
New Trends in Tropical Geometry
Organizers: Pierrick Bousseau (University of Georgia), Melody Chan (Brown University), Ilia Itenberg (Institut de Mathématiques de Jussieu - Paris Rive Gauche), Hannah Markwig (Eberhard-Karls-Universität Tübingen), LEAD Kris Shaw (University of Oslo) Tropical surfaces. Images courtesy of Lars Allermann.
Tropical surfaces. Images courtesy of Lars Allermann.Tropical geometry can be viewed as a degenerate version of algebraic geometry,where the role of algebraic varieties is played by certain polyhedral complexes. As the degeneration process, called tropicalization, preserves many fundamental properties, tropical geometry provides important bridges and an exchange of methods between algebraic geometry, symplectic geometry and convex geometry; these links have been extremely fruitful and gave rise to remarkable results during the last 20 years. The main focus of the program will be on the most significant recent developments in tropical geometry and its applications. The following topics are particularly influential in the area and will be central in the program:
- real aspects of tropical geometry;
- tropical mirror symmetry and non-Archimedean geometry;
- tropical phenomena in symplectic geometry;
- matroids, combinatorial and algebraic aspects;
- tropical moduli spaces;
- tropical geometry and A1-homotopy theory.
Updated on Mar 13, 2024 02:34 PM PDT -
Inverse Problems and Applications
Organizers: Fioralba Cakoni (Rutgers University), Maarten de Hoop (Rice University), Anna Gilbert (Yale University), Katya Krupchyk (University of California, Irvine), Matti Lassas (University of Helsinki), LEAD Gunther Uhlmann (University of Washington)
Inverse problems (IP) arise in all fields of science and technology where a cause for an observed or desired effect is sought. In the last 50 years or so there has been substantial progress in the mathematical understanding of these problems but many questions remain open. The mathematics of these problems involves many areas in Mathematics including PDE, differential geometry, integral geometry, probability, statistics, complex analysis, numerical analysis, mathematical physics, data science, etc. Since the 2010 program at the then-Mathematical Sciences Research Institute (now Simons Laufer Mathematical Sciences Institute), there has been significant progress in inverse problems; many of the advances can be traced back to that program. However, there are still deep open questions remaining as well, some of which are discussed in this proposal. New research topics include the connection between IP and machine learning, IP for nonlinear equations, IP for nonlocal operators, and connections between statistics and IP.
Updated on Feb 28, 2024 03:01 PM PST
|
|
Upcoming Programs |
