Current all workshops
-
Advances in Lie Theory, Representation Theory, and Combinatorics: Inspired by the work of Georgia M. Benkart
Organizers: Hélène Barcelo (MSRI / Simons Laufer Mathematical Sciences Institute (SLMath)), Ellen Kirkman (Wake Forest University), Gail Letzter (Retired ), Daniel Nakano (University of Georgia), Arun Ram (University of Melbourne)
This workshop will have a view to the future of a broad spectrum of topics including
- structure and classification of finite dimensional Lie algebras and superalgebras in characteristic p
- structure of infinite dimensional Lie algebras and their representations
- deformation theory of algebras, double constructions and elemental Lie algebras
- diagram algebras and combinatorial representation theory
- algebraic combinatorics of groups of Lie type:characters, Schur-Weyl duality, Bratteli diagrams, and McKay correspondences
- quantum groups and crystal bases, particularly for superalgebras and affine algebras
- examples of fusion categories arising from representations of Drinfeld doubles and other algebras
- cohomology for finite tensor categories with applications to its underlying geometry
This meeting will feature principal contributors in these areas in a celebration of the work of Georgia Benkart. With the same focus and tenacity that Georgia always had, we will strive to provide a conference full of beautiful mathematics, incredible inspiration, and the warmth of Georgia’s welcoming personality to our field and our community.
Updated on May 02, 2024 10:44 AM PDT
Upcoming all workshops
-
A Celebration for Women in Mathematics (2024) - May 12 Initiative
Organizers: Ini Adinya (University of Ibadan), Nasrin Altafi (Queen's University), Maria-Grazia Ascenzi (University of California Los Angeles), Shanna Dobson (University of California, Riverside), Malena Espanol (Arizona State University), Eleonore Faber (Karl-Franzens-Universität Graz; University of Leeds), Anna Fino (Università di Torino), Adi Glucksam (Northwestern University), Eloísa Grifo (University of Nebraska), Céleste Hogan (Texas Tech University), Ellen Kirkman (Wake Forest University), Kuei-Nuan Lin (Pennsylvania State University), Liangbing Luo (Lehigh University), LEAD Ornella Mattei (San Francisco State University), Claudia Miller (Syracuse University), Julia Plavnik (Indiana University), Claudia Polini (University of Notre Dame), Hema Srinivasan (University of Missouri), Špela Špenko (Université Libre de Bruxelles) "May 12 Initiative" Annual Workshop
"May 12 Initiative" Annual WorkshopThe Simons Laufer Mathematical Sciences Institute (SLMath) celebrates the "May 12 Initiative" with a panel discussion and social event open to all on the topic "Being a Woman in Mathematics". This is a hybrid event taking place on Zoom and in person at SLMath. This event is free and open to worldwide participation - please register online for Zoom link & details.
Updated on Apr 23, 2024 09:42 AM PDT -
Mathematically Advancing Young Undergraduates Program (MAY-UP) 2024
Updated on Apr 26, 2024 08:45 AM PDT -
Macaulay2, Computational Algebraic Geometry and String Theory
Organizers: David Eisenbud (University of California, Berkeley), Daniel Grayson, Anton Leykin (Georgia Institute of Technology), Andre Lukas (University of Oxford), Devlin Mallory (University of Utah), Liam McAllister (Cornell University), Karl Schwede (University of Utah), Michael Stillman (Cornell University)Updated on Apr 11, 2024 01:36 PM PDT -
Séminaire de Mathématiques Supérieures 2024: Flows and Variational Methods in Riemannian and Complex Geometry: Classical and Modern Methods (Montréal, Canada)
Organizers: Vestislav Apostolov (Université du Québec à Montréal), Eleonora Di Nezza (Institut de Mathématiques de Jussieu), Pengfei Guan (McGill University), Spiro Karigiannis (University of Waterloo), Julien Keller (Université du Québec à Montréal), Alina Stancu (Concordia University), Valentino Tosatti (New York University, Courant Institute)
This school will present various developments in Riemannian and Kähler geometry around the notion of curvature seen as a tool to describe and understand the geometry of the objects. The school will give graduate students the opportunity to learn key ideas and techniques of the field, with an emphasis on solidifying foundations in view of potential future research. The first week will be centered around the question of the existence of Kähler metrics with special curvature properties and the famous Yau-Tian-Donaldson conjecture. The second week will focus on geometric flows in Riemannian and complex geometry.
Updated on Mar 18, 2024 02:15 PM PDT -
MSRI-UP 2024: Mathematical Endocrinology
Organizers: Alexander Diaz-Lopez (Villanova University), Maria Mercedes Franco (Queensborough Community College (CUNY)), Rebecca Garcia (Colorado College), LEAD Candice Price (Smith College), Robin Wilson (Loyola Marymount University)The MSRI-UP summer program is designed to serve a diverse group of undergraduate students who would like to conduct research in the mathematical sciences.
In 2024, MSRI-UP will focus on Mathematical Endocrinology. The research program will be led by Dr. Erica J. Graham, Associate Professor in the Department of Mathematics at Bryn Mawr College.
Updated on Mar 07, 2024 11:11 AM PST -
Special Geometric Structures and Analysis (St. Mary's College)
Organizers: Costante Bellettini (University College London), LEAD Eleonora Di Nezza (Institut de Mathématiques de Jussieu), Song Sun (University of California, Berkeley) a Calabi-Yau manifold
a Calabi-Yau manifoldThis summer school will serve as an introduction to the SLMath program "Special geometric structures and analysis". There will be two mini-courses: one in Geometric Measure theory and the other in Microlocal Analysis. The aim is to give the basic notions of two subjects also treated during the program.
Updated on Apr 05, 2024 09:40 PM PDT -
Particle interactive systems: Analysis and computational methods (SLMath)
Organizers: LEAD Irene M. Gamba (University of Texas, Austin), Francois Golse (École Polytechnique), Qin Li (University of Wisconsin-Madison), Chiara Saffirio (Universität Basel)
This summer school will focus on the introductory notions related to the passage of Newtonian and quantum many-body dynamics to kinetic collisional models of Boltzmann flow models arising in statistical sciences in connection to model reductions when continuum macro dynamics arises; and their numerical schemes associated to transport of kinetic processes in classical and data driven mean field dynamics incorporating recent tools from computational kinetics and data science tools. There will be two sets of lectures: “From Newton to Boltzmann to Fluid dynamics”, and “Kinetic collisional theory in mean field regimes: analysis, discrete approximations, and applications”. Each lecture series will be accompanied by a collaboration session, led by the lecturer and teaching assistants. The purpose of the collaboration sessions is to encourage and strengthen higher-level thinking of the materials taught in the lectures and to direct further reading for interested students. Interactive learning activities will be conducted. For example, students will be given problem sets associated with the lectures and will work in small groups to discuss concepts and/or find solutions to assigned problems. The students will also be encouraged to give oral or poster presentations on their solutions or other materials relevant to the course.
Updated on Apr 10, 2024 02:59 PM PDT -
Introduction to Quantum-Safe Cryptography (IBM Zurich)
Organizers: Jonathan Bootle (IBM Zürich Research Laboratory), Luca De Feo (IBM Zürich Research Laboratory)
This two week summer school, jointly organized by SLMath with IBM Zurich, will introduce students to the mathematics and algorithms used in the design and analysis of quantum-safe cryptosystems. Each week will be dedicated to two of the four families of quantum-safe schemes.
Updated on May 01, 2024 08:53 AM PDT -
H-principle (Sendai, Japan)
Organizers: Emmy Murphy (Princeton University), Takashi Tsuboi (RIKEN Interdisciplinary Theoretical and Mathematical Sciences Program) The image of a large sphere isometrically embedded into a small space through a C^1 embedding. (Attributions: E. Bartzos, V. Borrelli, R. Denis, F. Lazarus, D. Rohmer, B. Thibert)
The image of a large sphere isometrically embedded into a small space through a C^1 embedding. (Attributions: E. Bartzos, V. Borrelli, R. Denis, F. Lazarus, D. Rohmer, B. Thibert)This two week summer school, jointly organized by SLMath with RIKEN, will introduce graduate students to the theory of h-principles. After building up the theory from basic smooth topology, we will focus on more recent developments of the theory, particularly applications to symplectic and contact geometry, fluid dynamics, and foliation theory.
h-principles in smooth topology (Emmy Murphy)
Riemannian geometry and applications to fluid dynamics (Dominik Inauen)
Contact and symplectic flexibility (Emmy Murphy)
Foliation theory and diffeomorphism groups (Takashi Tsuboi)Updated on Apr 17, 2024 10:55 AM PDT -
Koszul Duality in the Local Langlands Program (St. Mary's College)
Organizers: Clifton Cunningham (University of Calgary), LEAD Sarah Dijols (University of Calgary)
This summer school provides the mathematical background to recognize Koszul duality in representation theory. The school is especially oriented toward applications in the local Langlands program, with an emphasis on real groups. As Koszul duality patterns have been initially observed in the context of Hecke algebras, our school will also introduce the students to Hecke algebras and their categorifications.
Updated on Apr 12, 2024 11:27 PM PDT -
Stochastic Quantization (SLMath)
Organizers: Massimiliano Gubinelli (University of Oxford), Martina Hofmanova (Universität Bielefeld), LEAD Hao Shen (University of Wisconsin-Madison), Lorenzo Zambotti (Sorbonne Université)
This summer school will familiarize students with the basic problems of the mathematical theory of Euclidean quantum fields. The lectures will introduce some of its prominent models and analyze them via the so called “stochastic quantization” methods, involving recently developed stochastic and PDE techniques. This is an area which is highly interdisciplinary combining ideas ranging from the theory of partial differential equations, to stochastic analysis, to mathematical physics. Our goal is to bring together students who are perhaps familiar with some but not all of these subjects and teach them how to integrate these different tools to solve cutting-edge problems of Euclidean quantum field theory.
Updated on Apr 24, 2024 03:23 PM PDT -
Introduction to the Theory of Algebraic Curves (UC Berkeley)
Organizers: Izzet Coskun (University of Illinois, Chicago), Eric Larson (Brown University), LEAD Hannah Larson (University of California, Berkeley), Isabel Vogt (Brown University)
In the last few years, there have been extraordinary developments in many aspects of curve theory. Beginning with many examples in low genus, this summer school will introduce the participants to the background behind these developments in the following areas:
- moduli spaces of stable curves
- Brill–Noether theory
- the extrinsic geometry of the curves in projective space
We will also include an introduction to some open problems at the forefront of these active areas.
Updated on Apr 19, 2024 10:16 AM PDT -
Mathematics of General Relativity and Fluids (FORTH, Greece)
Organizers: LEAD Mihalis Dafermos (Princeton University), Grigorios Fournodavlos (University of Crete), Juhi Jang (University of Southern California), Igor Rodnianski (Princeton University) ALCF Visualization and Data Analytics Team; Adam Burrows and the Princeton Supernova Theory Group, Princeton University
ALCF Visualization and Data Analytics Team; Adam Burrows and the Princeton Supernova Theory Group, Princeton UniversityThis summer school will give an accessible introduction to the mathematical study of general relativity, a field which in the past has had barriers to entry due to its interdisciplinary nature, and whose study has been concentrated at specific institutions, to a wider audience of students studying at institutions throughout the U.S., Europe and Greece. Another goal of the summer school will be to demonstrate the common underlying mathematical themes in many problems which traditionally have been studied by separate research communities.
Updated on Mar 19, 2024 04:24 PM PDT -
Multigraded and differential graded methods in commutative algebra (St. Mary's College)
Organizers: Michael Brown (Auburn University), Claudia Miller (Syracuse University) Product of projective lines embedded in projective 3-space
Product of projective lines embedded in projective 3-spaceThis summer graduate school focuses on modern homological techniques in commutative algebra, specifically those involving multigraded and differential graded structures. These topics have a long and rich history, but neither is generally covered in graduate courses. Moreover, recent developments have exhibited exciting interplay between the two subjects.
The purpose of the school is to introduce the participants to modern themes on these topics, including Koszul duality for toric varieties and differential graded algebra structures on resolutions. The school will consist of two lectures each day and carefully planned problem sessions designed to reinforce the foundational material, with an emphasis on using computational tools such as the symbolic algebra program Macaulay2.
Updated on Apr 16, 2024 12:43 PM PDT -
Analysis of Partial Differential Equations (Okinawa Institute of Science and Technology)
Organizers: Ugur Abdulla (Okinawa Institute of Science and Technology), Gui-Qiang Chen (University of Oxford)This two week summer school, jointly organized by SLMath with OIST, will offer the following two mini-courses:
- Measure-theoretical analysis, divergence-measure fields, and nonlinear PDEs of divergence form
This course will present some recent developments in the theory of divergence-measure fields via measure-theoretic analysis and its applications to the analysis of nonlinear PDEs of conservative form – nonlinear conservation laws. - Perron’s method and Wiener-type criteria in the potential theory of elliptic and parabolic PDEs
This course will present some recent developments precisely characterizing the regularity of the point at ∞ for second order elliptic and parabolic PDEs and broadly extending the role of the Wiener test in classical analysis.
Updated on Apr 19, 2024 12:54 PM PDT - Measure-theoretical analysis, divergence-measure fields, and nonlinear PDEs of divergence form
-
Mathematical Spin Glass Theory (Courant, NY)
Organizers: Antonio Auffinger (Northwestern University), Wei-Kuo Chen (University of Minnesota), LEAD Eliran Subag (Weizmann Institute of Science)
While their original aim was to explain the strange behavior of certain magnetic alloys, the study of spin glass models has led to a far-reaching and beautiful physical theory whose techniques have been applied to a myriad of problems in theoretical computer science, statistics, optimization and biology. As many of the physical predictions can be formulated as purely mathematical questions, often extremely hard, about large random systems in high dimensions, in recent decades a new area of research has emerged in probability theory around these problems.
Mathematically, a mean-field spin glass model is a Gaussian process (random function) on the discrete hypercube or the sphere in high dimensions. A fundamental challenge in their analysis is, roughly speaking, to understand the size and structure of their super-level sets as the dimension tends to infinity, which are often studied through smooth objects like the free energy and Gibbs measure whose origin is in statistical physics. The aim of the summer school is to introduce students to landmark results on the latter while emphasizing the techniques and ideas that were developed to obtain them, as well as exposing the students to some recent research topics.
Updated on Apr 19, 2024 03:00 PM PDT -
Connections Workshop: New Frontiers in Curvature & Special Geometric Structures and Analysis
Organizers: Sun-Yung Chang (Princeton University), Lan-Hsuan Huang (University of Connecticut), Chikako Mese (Johns Hopkins University), Ilaria Mondello (Université Paris-Est Créteil Val-de-Marne), LEAD Guofang Wei (University of California, Santa Barbara), LEAD Xuwen Zhu (Northeastern University) Geosurface
GeosurfaceThis three-day workshop will consist of various talks given by prominent female mathematicians on topics of differential geometry and geometric analysis. These will be appropriate for graduate students, post-docs, and researchers in areas related to the two programs. The workshop will also include activities to promote interaction and connection between participants. This workshop is open to all mathematicians.
Updated on Apr 30, 2024 11:01 AM PDT -
Introductory Workshop: New Frontiers in Curvature
Organizers: Ailana Fraser (University of British Columbia), Karsten Grove (University of Notre Dame), Richard Schoen (Stanford University), Catherine Searle (Wichita State University), LEAD Lu Wang (Yale University) The spatial Schwarzschild space with minimal surface boundary foliated by the inverse mean curvature flow
The spatial Schwarzschild space with minimal surface boundary foliated by the inverse mean curvature flowThis workshop will include introductory lectures on each of the four main topics of the program: geometric flows, geometric problems in mathematical relativity, global Riemannian geometry, and minimal submanifolds. The workshop will also have semi-expository lectures on recent advances and breakthroughs involving interactions between the four main topics. This will set the stage and provide important context for the semester-long program itself.
Updated on Apr 30, 2024 11:03 AM PDT -
Introductory Workshop: Special Geometric Structures and Analysis
Organizers: Anda Degeratu (Universität Stuttgart), LEAD Eleonora Di Nezza (Institut de Mathématiques de Jussieu), Luca Spolaor (University of California, San Diego), Song Sun (University of California, Berkeley)
This workshop aims to prepare the participants for the main program: Special Geometric Structures and Analysis.
There will be introductory lectures to recent results in geometry and analysis; more precisely in Kähler geometry, special holonomy, microlocal analysis and geometric measure theoryUpdated on Apr 30, 2024 11:05 AM PDT -
Recent progress on geometric analysis and Riemannian geometry
Organizers: LEAD Lan-Hsuan Huang (University of Connecticut), Andre Neves (University of Chicago), Richard Schoen (Stanford University), LEAD Catherine Searle (Wichita State University), Guofang Wei (University of California, Santa Barbara) <p>The Hopf fibration of <span class="math-tex">\(S^3 \space by \space S^1\)</span></p>
<p>The Hopf fibration of <span class="math-tex">\(S^3 \space by \space S^1\)</span></p>This workshop will bring together researchers at the frontiers of geometric analysis and Riemannian geometry, with a focus on recent advances on geometric flows, geometric problems in mathematical relativity, global Riemannian geometry, and minimal submanifolds. These areas have shown highly intriguing interactions in recent years and we expect this workshop will provide a unique opportunity to facilitate these emerging links.
Updated on Apr 30, 2024 11:06 AM PDT -
Geometry and analysis of special structures on manifolds
Organizers: Anna Fino (Università di Torino), Mark Haskins (Duke University), Tristan Riviere (ETH Zurich), Neshan Wickramasekera (University of Cambridge)
The analysis of solutions to nonlinear geometric PDEs with higher-dimensional singular sets has seen some notable recent advances, but many fundamental questions still remain open. This workshop will bring together a wide array of researchers working in differential geometry, gauge theory, nonlinear PDEs, microlocal analysis, the calculus of variations and geometric measure theory, with the goal of describing recent advances, advertising recent technical breakthroughs and forging new connections.
Updated on Apr 30, 2024 11:08 AM PDT -
Hot Topics: Life after the Telescope Conjecture
Organizers: LEAD Agnes Beaudry (University of Colorado), Michael Hill (University of California, Los Angeles), Vesna Stojanoska (University of Illinois at Urbana-Champaign)
In June 2023, Burklund, Hahn, Levy, and Schlank surprised the homotopy theory community when they announced a disproof of Ravenel's Telescope Conjecture, a fundamental problem of homotopy theory which had been open for 40 years and was believed to be out of reach. The disproof of the Telescope Conjecture combines some of the most exciting recent developments in homotopy theory. This includes fundamental work on red-shift phenomena and descent in algebraic K-theory, trace methods based on a novel approach to topological Hochschild and cyclic homology, ambidexterity in chromatic homotopy theory, and more.
The workshop will explore this amazing body of work, culminating in its synthesis and ingenious application to disprove the Telescope Conjecture.
Updated on Apr 30, 2024 11:09 AM PDT -
Connections Workshop: Probability and Statistics of Discrete Structures
Organizers: Christina Goldschmidt (University of Oxford), Po-Ling Loh (University of Cambridge), Kavita Ramanan (Brown University), Dana Randall (Georgia Institute of Technology), LEAD Nike Sun (Massachusetts Institute of Technology) AI-generated interpretation of a random network
AI-generated interpretation of a random networkThis two-day workshop will bring together researchers from discrete mathematics, probability theory, theoretical computer science, and statistics to explore topics at their interface. The focus will be on probability and statistics of random discrete structures, as well as their applications, including in computer science and physical systems. The workshop will celebrate academic and gender diversity, bringing together women and men at junior and senior levels of their careers from mathematics, physics, and computer science.
Updated on May 30, 2023 03:32 PM PDT -
Introductory Workshop: Probability and Statistics of Discrete Structures
Organizers: Louigi Addario-Berry (McGill University), LEAD Shankar Bhamidi (University of North Carolina), Christina Goldschmidt (University of Oxford), Dana Randall (Georgia Institute of Technology), Perla Sousi (University of Cambridge), Remco van der Hofstad (Technische Universiteit Eindhoven) Visualization of a network constructed using simple probabilistic rules, showing the emergence of hubs and other macroscopic network phenomenon. From https://graph-tool.skewed.de
Visualization of a network constructed using simple probabilistic rules, showing the emergence of hubs and other macroscopic network phenomenon. From https://graph-tool.skewed.deNetworks, graph driven algorithms, and dynamics on graphs such as epidemics, random walks and centrality measures all play a major role, both in our daily lives as well as many scientific and engineering disciplines. This introductory workshop will bring together experts and junior researchers in combinatorics, probability, and statistics to share a broad vision of major challenges and objectives, with a primary focus on models of random graphs and their limits, network inference, dynamic processes on networks and algorithms and optimization on random structures.
Updated on May 30, 2023 11:38 AM PDT -
Connections Workshop: Extremal Combinatorics
Organizers: Julia Böttcher (London School of Economics and Political Science), Anita Liebenau (University of New South Wales), LEAD Maya Stein (Universidad de Chile)
The purpose of this workshop is to bring together promising early-career researchers in extremal combinatorics who are women or from underrepresented minorities so that they can meet with, forge connections with, and be inspired by the leading figures in the area. The workshop will include lectures, time for collaborative research, and an informal panel discussion session among female and minority researchers on career issues.
Updated on Apr 04, 2023 08:43 AM PDT -
Introductory Workshop - Graph Theory: Extremal, Probabilistic and Structural
Organizers: LEAD Penny Haxell (University of Waterloo), Michael Krivelevich (Tel Aviv University), Alex Scott (University of Oxford)
This workshop will feature leading experts in several major areas of graph theory, including extremal, probabilistic and structural aspects of the field. Introductory lectures will form an important part of the program, providing background and motivation, and aimed at a general mathematical audience. Complementing these, research talks will share exciting recent developments in graph theory.
Updated on Mar 31, 2023 03:48 PM PDT -
Hot Topics: Interactions between Harmonic Analysis, Homogeneous Dynamics, and Number Theory
Organizers: Dubi Kelmer (Boston College), LEAD Amir Mohammadi (University of California, San Diego), Hong Wang (New York University, Courant Institute)
In recent years techniques from harmonic analysis viz. projection theorems have found striking applications in finitary analysis on homogenous spaces. Such quantitative results have many potential applications to analytic number theory. This workshop will bring together researchers in these areas to further explore these connections.
Updated on Apr 12, 2024 09:01 AM PDT -
Algebraic and Analytic Methods in Combinatorics
Organizers: Janos Pach (Alfréd Rényi Institute of Mathematics), Andrew Suk (University of California, San Diego), LEAD Yufei Zhao (Massachusetts Institute of Technology) A degree 7 curve passing through 35 points in the plane
A degree 7 curve passing through 35 points in the planeMany exciting breakthroughs in combinatorics involve innovative applications of techniques from a wide range of areas such as harmonic analysis, polynomial and linear algebraic methods, spectral graph theory, and representation theory. This workshop will present recent developments in this area and facilitate discussions of research problems.
Updated on Jul 19, 2023 04:10 PM PDT -
Detection, Estimation, and Reconstruction in Networks
Organizers: Po-Ling Loh (University of Cambridge), Gabor Lugosi (ICREA), Sofia Olhede (École Polytechnique Fédérale de Lausanne (EPFL)), Roberto Oliveira (Institute of Pure and Applied Mathematics (IMPA)), LEAD Miklos Racz (Northwestern University) Recovering communities in a network.
Recovering communities in a network.In a growing number of applications, one needs to analyze and interpret data coming from massive networks. The statistical problems arising from such applications lead to important mathematical challenges: building novel probabilistic models, understanding the possibilities and limitations for statistical detection and inference, designing efficient algorithms, and understanding the inherent limitations of fast algorithms. The workshop will bring together leading researchers in combinatorial statistics, machine learning, and random graphs in the hope of cross-fertilization of ideas.
Updated on Aug 05, 2023 10:06 AM PDT -
Statistical Optimal Transport (St. Mary's College)
Organizers: LEAD Promit Ghosal (Brandeis University), Jonathan Niles-Weed (New York University, Courant Institute), Marcel Nutz (Columbia University)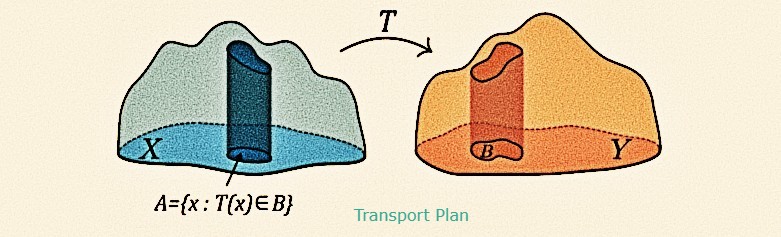
This summer school offers an exceptional opportunity for participants to delve into the intricate realm of statistical optimal transport theory. This captivating field stands at the crossroads of multiple disciplines, drawing from a rich tapestry of mathematical insights from diverse subjects, including partial differential equations, stochastic analysis, convex geometry, statistics, and machine learning, crafting a vibrant and interdisciplinary landscape. The foremost objective of this summer school is to create a dynamic learning environment that unites students from diverse backgrounds such as PDE theory, probability, or optimal transport.
Updated on Mar 20, 2024 02:04 PM PDT -
Noncommutative Algebraic Geometry
Organizers: Pieter Belmans (University of Luxembourg), Lander Hermans (Universiteit Antwerp), Wendy Lowen (Universiteit Antwerpen), Arne Mertens (Universiteit Antwerp), Michel VAN DEN BERGH (Hasselt University), Špela Špenko (Université Libre de Bruxelles)Created on Apr 03, 2024 05:26 PM PDT -
Computer Assisted Proofs in Applied Mathematics (SLMath)
Organizers: LEAD Jonathan Jaquette (New Jersey Institute of Technology), Evelyn Sander (George Mason University)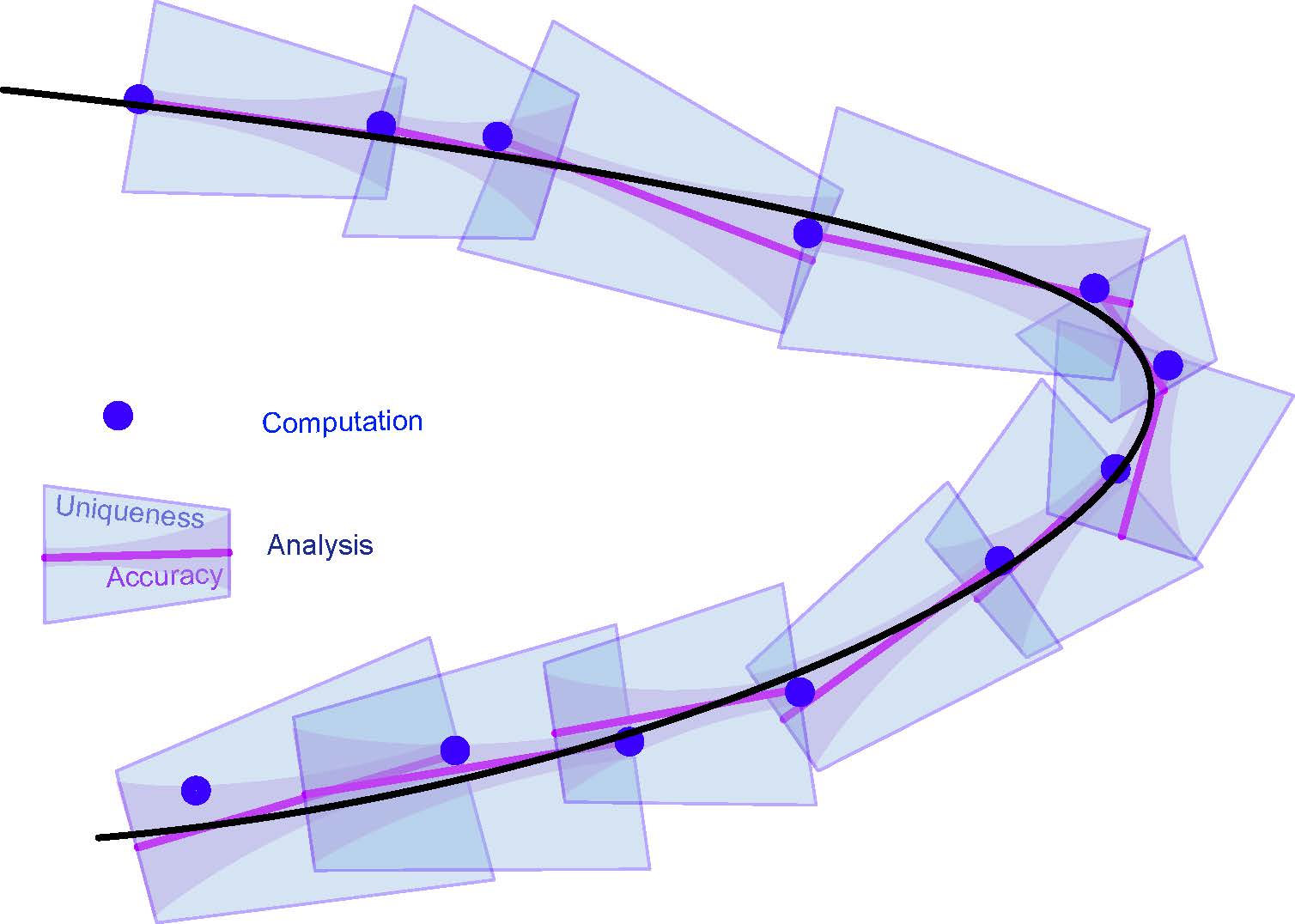
One of the core elements of applied mathematics is mathematical modeling consisting of nonlinear equations such as ODEs, and PDEs. A fundamental difficulty which arises is that most nonlinear models cannot be solved in closed form. Computer assisted proofs are at the forefront of modern mathematics and have led to many important recent mathematical advances. They provide a way of melding analytical techniques with numerical methods, in order to provide rigorous statements for mathematical models that could not be treated by either method alone. In this summer school, students will review standard computational and analytical techniques, learn to combine these techniques with more specialized methods of interval arithmetic, and apply these methods to establish rigorous results in otherwise intractable problems
Updated on Apr 08, 2024 08:55 AM PDT -
Geometry and Dynamics in Higher Rank Lie Groups (St. Mary's College)
Organizers: Richard Canary (University of Michigan), Sara Maloni (University of Virginia), Wenyu Pan (University of Toronto), Cagri Sert (University of Zurich), LEAD Tengren Zhang (National University of Singapore) <p>Flats and hyperbolic planes in a higher rank symmetric space</p> Drawn by Steve Trettel.
<p>Flats and hyperbolic planes in a higher rank symmetric space</p> Drawn by Steve Trettel.Lie groups are central objects in modern mathematics; they arise as the automorphism groups of many homogeneous spaces, such as flag manifolds and Riemannian symmetric spaces. Often, one can construct manifolds locally modelled on these homogeneous spaces by taking quotients of their subsets by discrete subgroups of their automorphism groups. Studying such discrete subgroups of Lie groups is an active and growing area of mathematical research. The objective of this summer school is to introduce young researchers to a class of discrete subgroups of Lie groups, called Anosov subgroups.
Updated on Apr 18, 2024 08:43 AM PDT -
Topological and Geometric Structures in Low Dimensions (SLMath)
Organizers: LEAD Kenneth Bromberg (University of Utah), Kathryn Mann (Cornell University) <p>Laminations arise naturally in hyperbolic geometry and (pseudo-) Anosov flows [Image by Jeffrey Brock]</p>
<p>Laminations arise naturally in hyperbolic geometry and (pseudo-) Anosov flows [Image by Jeffrey Brock]</p>This school will serve as an introduction to the SLMath semester “Topological and Geometric Structures in Low-Dimensions”. The school consists of two mini-courses: one on Teichmüller Theory and Hyperbolic 3-Manifolds and the other on Anosov Flows on Geometric 3-Manifolds. Both topics lie at the interface of low-dimensional geometric topology (specifically, surfaces, foliations, and 3-manifolds) and low-dimensional dynamics. The first course will be targeted towards students who have completed the standard first year graduate courses in geometry, topology, and analysis while the second course will geared towards more advanced students who are closer to beginning research. However, we expect that all students will benefit from both courses.
Updated on Mar 21, 2024 09:48 AM PDT
Past all workshops
-
Workshop Recent Developments in Commutative Algebra
Organizers: Daniel Erman (University of Michigan), Linquan Ma (Purdue University), LEAD Karl Schwede (University of Utah), Karen Smith (University of Michigan), Andrew Snowden (University of Michigan), Irena Swanson (Purdue University)Many long-standing conjectures in commutative algebra have been solved in recent years, often through the introduction of new methods that are quickly becoming central to the field. This workshop will bring together a wide array of researchers in commutative algebra and related fields, with the goal of forging new connections among topics, and with a particular emphasis on transformative new methods.
Updated on Apr 19, 2024 12:08 PM PDT -
Workshop Recent Developments in Noncommutative Algebraic Geometry
Organizers: Arend Bayer (University of Edinburgh), Graham Leuschke (Syracuse University), Alexander Polishchuk (University of Oregon), Susan Sierra (University of Edinburgh), Gregory Stevenson (Aarhus University), Špela Špenko (Université Libre de Bruxelles) Optical illusion staircase
Optical illusion staircaseThis workshop will give an overview of recent developments in non-commutative algebraic geometry, including NC projective AG, NC resolutions, semiorthogonal decompositions, enhancements of derived categories, and connections to homological mirror symmetry, to enumerative AG, to moduli spaces and to birational geometry. It will in particular focus on speakers who have built new bridges between these topics.
Updated on Apr 12, 2024 11:42 AM PDT -
Workshop Critical Issues in Mathematics Education 2024: Bringing Innovation to Scale: Teaching-Focused Faculty as Change Agents
Organizers: Debra Carney (Colorado School of Mines), Dave Kung (St. Mary's College of Maryland), P. Gavin LaRose (University of Michigan), Mary Pilgrim (San Diego State University), Chris Rasmussen (San Diego State University), Natasha Speer (University of Maine), Cristina Villalobos (University of Texas Rio Grande Valley)
The undergraduate mathematics education system remains a huge barrier to college completion and to equity in higher education. The problem in entry level mathematics courses is not a lack of innovation. Numerous projects and institutions have created, piloted, and occasionally replicated effective reform efforts that overcame particular challenges, like the need to improve pedagogical practices or attend to gender equity. The biggest barrier to systemic reform – implementing many of these research-backed innovations at scale – is a structural one, particularly at large research-focused institutions. This workshop will bring together a group of stakeholders to explore a new avenue for change, the rise of teaching-focused faculty at research-intensive institutions who increasingly influence introductory coursework. By creating a network that connects these faculty across institutions, change at scale across 50, 100, or even more institutions becomes possible – on issues ranging from pedagogy to equity to curricular innovation. Creating such structures would also allow for bringing future innovations to scale much more quickly than is currently possible.
Updated on Apr 19, 2024 06:56 AM PDT -
Workshop Hot Topics: Artin Groups and Arrangements - Topology, Geometry, and Combinatorics
Organizers: Christin Bibby (Louisiana State University), Ruth Charney (Brandeis University), Giovanni Paolini (Università di Bologna), Mario Salvetti (Università di Pisa)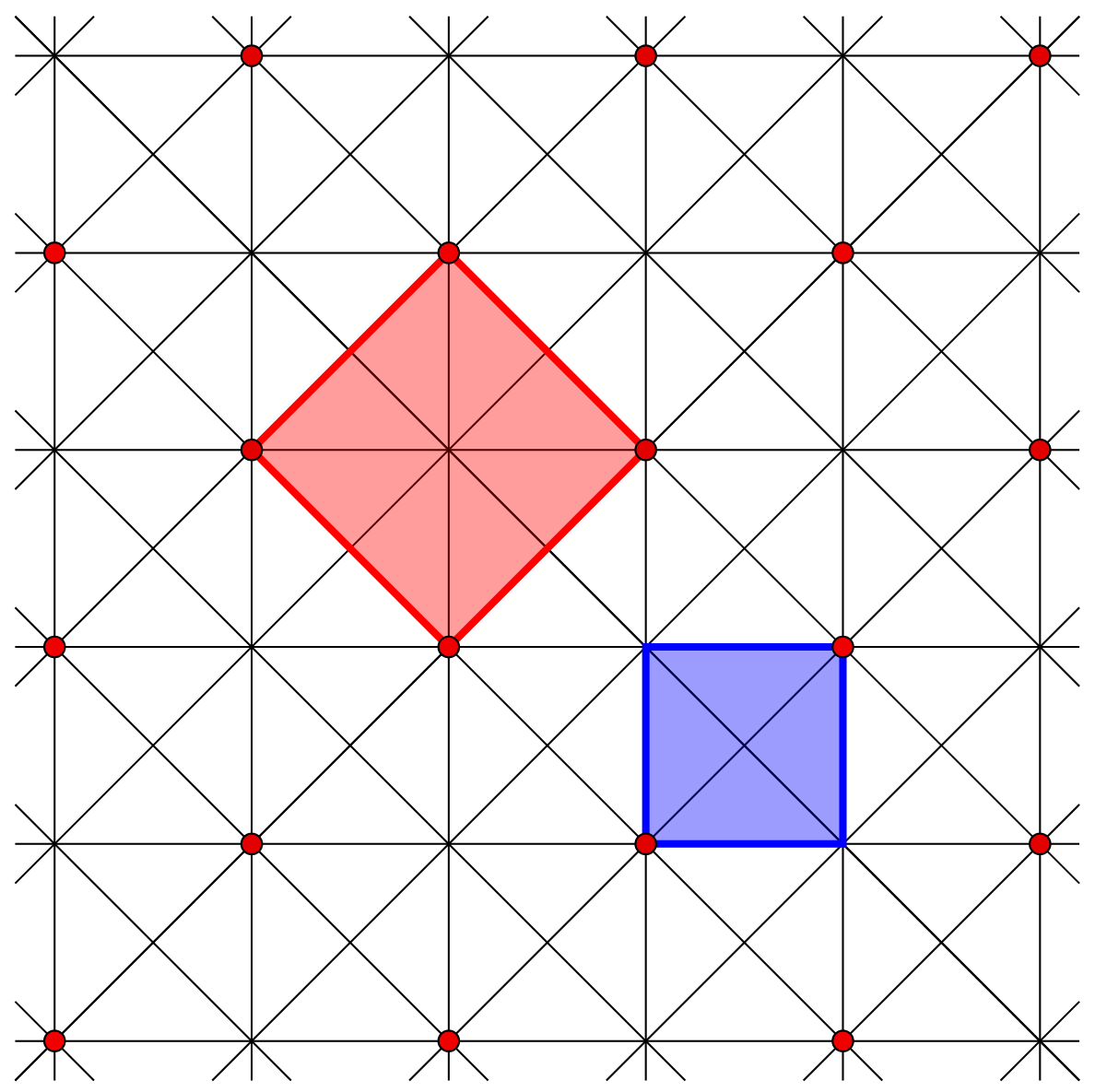 The affine line arrangement of type C with different lattices and toric arrangements arising from it.
The affine line arrangement of type C with different lattices and toric arrangements arising from it.This workshop brings together experts from different areas to discuss and foster collaboration on several topics of current interest related to Artin groups such as the K(π, 1) conjecture, hyperplane arrangements and abelian arrangements, combinatorial structures associated with dual Coxeter systems, and complexes of nonpositive curvature.
Updated on Mar 14, 2024 11:29 AM PDT -
Workshop Introductory Workshop: Noncommutative Algebraic Geometry
Organizers: Nicolas Addington (University of Oregon), LEAD David Favero (University of Minnesota), Wendy Lowen (Universiteit Antwerpen), Alice Rizzardo (University of Liverpool) A paper fortune teller illustrating the Atiyah flop.
A paper fortune teller illustrating the Atiyah flop.This introductory workshop will consist of a combination of minicourses addressing core topics in noncommutative algebraic geometry and research lectures describing recent developments in the field. The workshop will focus on subjects connected to algebraic geometry, category theory, and mirror symmetry such as categorical and noncommutative resolutions, deformation theory, derived categories in algebraic geometry, derived algebraic geometry, infinity categories, and enumerative geometry.
Updated on Feb 12, 2024 02:24 PM PST -
Workshop Connections Workshop: Noncommutative Algebraic Geometry
Organizers: Rina Anno (Kansas State University), Elizabeth Gasparim (Universidad Católica del Norte), LEAD Alice Rizzardo (University of Liverpool)
This two-day workshop will feature the work of mathematicians in noncommutative geometry who identify as women or another marginalized gender. The talks will be appropriate for graduate students, post-docs, and researchers in areas related to the program. This meeting aims to support young researchers.
The workshop will focus on recent developments in noncommutative algebraic geometry including Derived Algebraic Geometry, Categorical and Noncommutative Resolutions, Deformation Theory, and Enumerative Geometry.
The format will include plenary talks, a poster session, panel discussions, as well as the opportunity for informal discussions and connections in noncommutative geometry. The workshop is open to all mathematicians, and members of historically excluded groups and identities are especially encouraged to attend.
Updated on Feb 12, 2024 02:19 PM PST -
Workshop Introductory Workshop: Commutative Algebra
Organizers: Srikanth Iyengar (University of Utah), Claudia Miller (Syracuse University), Claudia Polini (University of Notre Dame), LEAD Anurag Singh (University of Utah)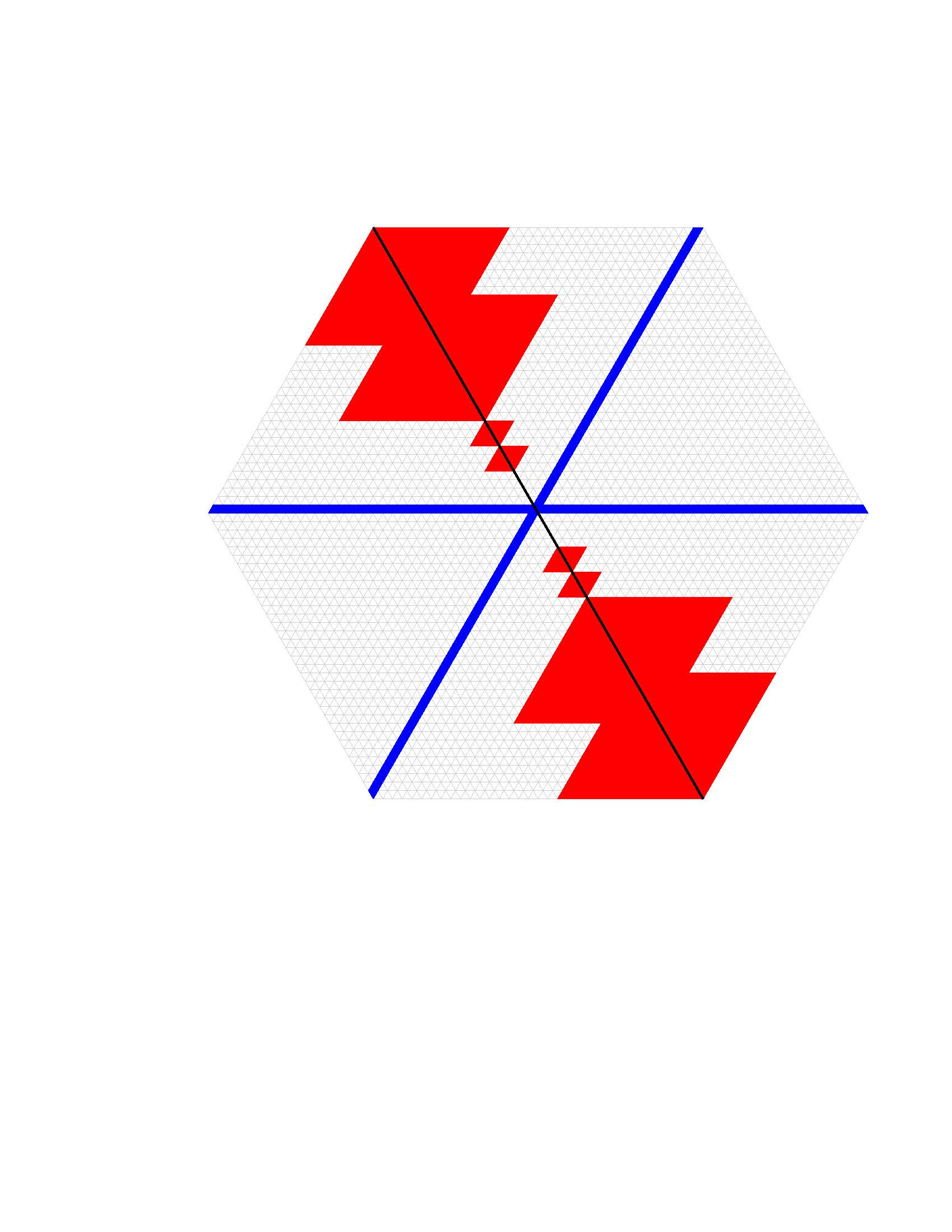 Fractal behavior of local cohomology. For details, see arXiv:2210.03656 by Gao and Raicu
Fractal behavior of local cohomology. For details, see arXiv:2210.03656 by Gao and RaicuThe Introductory Workshop will feature lecture series devoted to some recent breakthrough results in commutative algebra, and to new developments in core areas of the field. It will also highlight links to other areas such as arithmetic geometry, representation theory, noncommutative geometry, and singularity theory.
Updated on Jan 26, 2024 10:38 AM PST -
Workshop Connections Workshop: Commutative Algebra
Organizers: Christine Berkesch (University of Minnesota), Louiza Fouli (New Mexico State University), Maria Evelina Rossi (Università di Genova), LEAD Alexandra Seceleanu (University of Nebraska)This two-day workshop will feature the work of mathematicians in commutative algebra who identify as women or another marginalized gender. The talks will be appropriate for graduate students, post-docs, and researchers in areas related to the program. This meeting aims to support young researchers. The format will include plenary talks, poster sessions, panel discussions, as well as the opportunity for informal discussions and connections. The workshop is open to all mathematicians, and members of historically excluded groups and identities are especially encouraged to attend.
Updated on Jan 19, 2024 11:42 AM PST -
Workshop Hot Topics: Recent Progress in Deterministic and Stochastic Fluid-Structure Interaction
Organizers: Martina Bukac (University of Notre Dame), Suncica Canic (University of California, Berkeley), LEAD Jeffrey Kuan (University of Maryland), Justin Webster (University of Maryland, Baltimore County)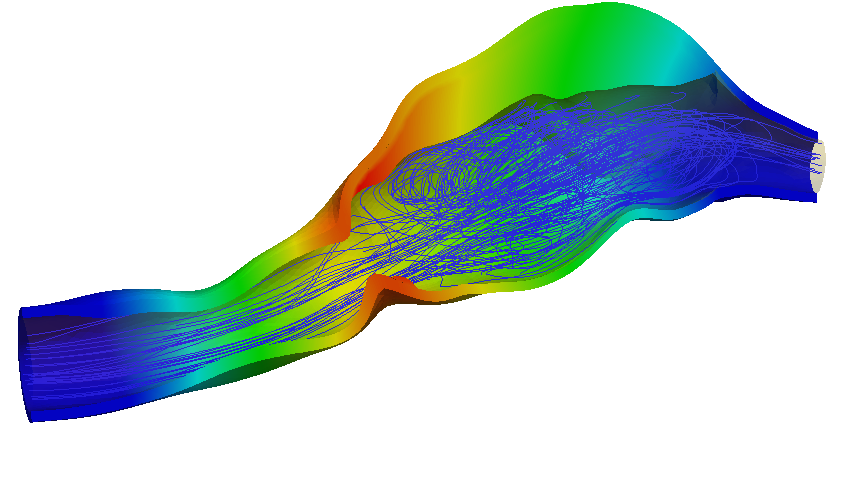 Blood flow and structure displacement in an Aortic Abdominal Aneurysm
Blood flow and structure displacement in an Aortic Abdominal AneurysmThis workshop will focus on the coupled dynamical interaction between fluids and elastic/poroelastic structures, with an emphasis on the most recent and cutting-edge mathematical advances in deterministic and stochastic fluid-structure interaction. The goal of this workshop is to bring together a diverse group of mathematicians in the fields of analysis, modeling, numerics, stochastics, and real-world applications in order to showcase an interdisciplinary approach to the study of coupled fluid-structure systems. A major component of this workshop will be to encourage active participation of early career researchers, such as graduate students and postdocs, and foster synergistic collaboration with established leaders in the field.
Updated on Jan 11, 2024 11:47 PM PST -
Workshop Algorithms, Approximation, and Learning in Market and Mechanism Design
Organizers: LEAD Martin Bichler (TU München), LEAD Péter Biró (KRTK – Institute of Economics)
The workshop is aimed at exploring core subjects in the field of market and mechanism design, such as the design of non-convex auction markets, the design of matching markets with preferences, algorithmic mechanism design, and learning in games. These topics are interrelated and deeply rooted in mathematics and computer science. Each day of the 4-day workshop is devoted to one of these topics with talks by leading scholars in the field and panel discussions on major open problems.
Updated on Nov 13, 2023 11:20 AM PST -
Workshop Modern Math 2023
Updated on May 26, 2023 09:14 AM PDT -
Workshop Randomization, Neutrality, and Fairness
Organizers: LEAD Jonathan Mattingly (Duke University), Berk Ustun (University of California, San Diego), Rachel Ward (University of Texas at Austin)This workshop will look at the idea of fairness and neutrality in algorithms and decision-making. How it relates to the idea of randomization and how randomization can be employed in the pursuit of neutrality and fairness. The goal is both to bring together state-of-the-art research and explore the implications and limitations of the deployment in the real world.
Updated on Oct 27, 2023 08:35 AM PDT -
Workshop Hot Topics: MIP* = RE and the Connes’ Embedding Problem
Organizers: Michael Chapman (New York University, Courant Institute), Anand Natarajan (Massachusetts Institute of Technology), William Slofstra (University of Waterloo), John Wright (University of Texas, Austin), Henry Yuen (Columbia University)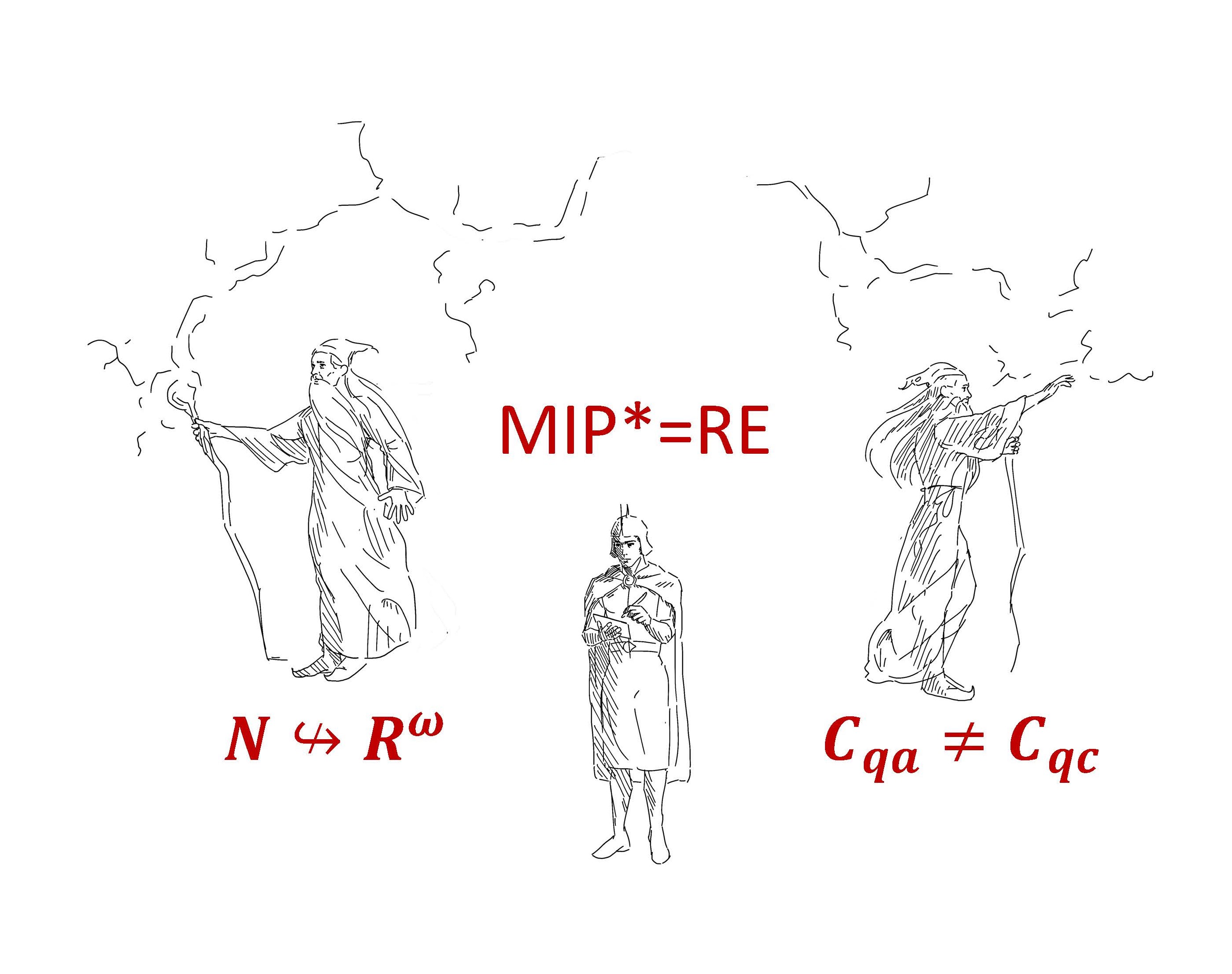 Drawing by Tina Zhang.
Drawing by Tina Zhang.This workshop is about the recent MIP*=RE result from quantum computational complexity, and the resulting resolution of the Connes embedding problem from the theory of von Neumann algebras. MIP*=RE connects the disparate areas of computational complexity theory, quantum information, operator algebras, and approximate representation theory. The aim of this workshop is to bridge this divide, by giving an in-depth exposition of the techniques used in the proof of MIP*=RE, and highlighting perspectives on the MIP*=RE result from operator algebras and approximate representation theory. In particular, this workshop will highlight connections with group stability, something that has not been covered in previous workshops. In addition to increasing understanding of the MIP*=RE proof, we hope that this will open up further applications of the ideas behind MIP*=RE in operator algebras.
Updated on Oct 25, 2023 11:46 AM PDT -
Workshop Introductory Workshop: Mathematics and Computer Science of Market and Mechanism Design
Organizers: Scott Kominers (Harvard Business School), Paul Milgrom (Stanford University), Alvin Roth (Stanford University), Eva Tardos (Cornell University)
This workshop is multifaceted. In addition to familiarizing graduate students and other junior participants to the topics of the program, the workshop will also reinforce common ground and language among computer scientists and economists and provide an on-ramp introduction for interested mathematicians.
Updated on Sep 25, 2023 01:08 PM PDT -
Workshop Connections Workshop: Mathematics and Computer Science of Market and Mechanism Design
Organizers: Michal Feldman (Tel-Aviv University), LEAD Nicole Immorlica (Microsoft Research)
The Connections Workshop will consist of invited talks from leading researchers at all career stages in the field of market design. Particular attention will be paid to real-world applications. There will also be an AMA focused on career paths with highly visible individuals in the field, and a social event intended to help workshop attendees network with each other.
Updated on Sep 27, 2023 09:35 AM PDT -
Workshop Introductory Workshop: Algorithms, Fairness, and Equity
Organizers: Vincent Conitzer (Carnegie Mellon University), LEAD Moon Duchin (Tufts University), Wesley Pegden (Carnegie Mellon University), Dana Randall (Georgia Institute of Technology), LEAD Soledad Villar (Johns Hopkins University) Image generated by an AI process.
Image generated by an AI process.In this workshop, we will bring together speakers who are engaged in the active areas of scholarship around algorithmic fairness, the disparate impacts of facially impartial systems, and the ways that algorithms can be enmeshed in governance and decisionmaking—for better and worse. The speakers will introduce themes that will be picked up throughout the semester program on "Algorithms, Fairness, and Equity."
Updated on Oct 18, 2023 09:08 AM PDT -
Workshop Connections Workshop: Algorithms, Fairness, and Equity
Organizers: Vincent Conitzer (Carnegie Mellon University), LEAD Rachel Cummings (Columbia University), Ana-Andreea Stoica (Max Planck for Intelligent Systems)
The Connections Workshop will welcome participants of all genders and identities, with the scope of fostering a sense of community, amplifying voices of those who identify as women, and providing avenues to allies to be helpful. The workshop particularly aims to increase visibility among junior women in fields adjacent to the topics of the general program, including but not limited to game-theoretic fairness, mechanism design, partition, networks, redistricting, and fairness in machine learning. This two-day workshop will include keynote speakers, lightning talks from participants, panel discussions on career advancement, breakout sessions by research areas, opportunities for networking, and other mentoring activities.
Updated on Aug 30, 2023 02:37 PM PDT -
Summer Graduate School Foundations and Frontiers of Probabilistic Proofs (Zürich, Switzerland)
Organizers: Alessandro Chiesa (École Polytechnique Fédérale de Lausanne (EPFL)) Several executions of a 3-dimensional sumcheck protocol with a random order of directions (thanks to Dev Ojha for creating the diagram)
Several executions of a 3-dimensional sumcheck protocol with a random order of directions (thanks to Dev Ojha for creating the diagram)Proofs are at the foundations of mathematics. Viewed through the lens of theoretical computer science, verifying the correctness of a mathematical proof is a fundamental computational task. Indeed, the P versus NP problem, which deals precisely with the complexity of proof verification, is one of the most important open problems in all of mathematics.
The complexity-theoretic study of proof verification has led to exciting reenvisionings of mathematical proofs. For example, probabilistically checkable proofs (PCPs) admit local-to-global structure that allows verifying a proof by reading only a minuscule portion of it. As another example, interactive proofs allow for verification via a conversation between a prover and a verifier, instead of the traditional static sequence of logical statements. The study of such proof systems has drawn upon deep mathematical tools to derive numerous applications to the theory of computation and beyond.
In recent years, such probabilistic proofs received much attention due to a new motivation, delegation of computation, which is the emphasis of this summer school. This paradigm admits ultra-fast protocols that allow one party to check the correctness of the computation performed by another, untrusted, party. These protocols have even been realized within recently-deployed technology, for example, as part of cryptographic constructions known as succinct non-interactive arguments of knowledge (SNARKs).
This summer school will provide an introduction to the field of probabilistic proofs and the beautiful mathematics behind it, as well as prepare students for conducting cutting-edge research in this area.
Updated on Oct 20, 2023 01:17 PM PDT -
Summer Graduate School Mathematics of Big Data: Sketching and (Multi-) Linear Algebra (IBM Almaden)
Organizers: Kenneth Clarkson (IBM Research Division), Lior Horesh (IBM Thomas J. Watson Research Center), Misha Kilmer (Tufts University), Tamara Kolda (MathSci.ai), Shashanka Ubaru (IBM Thomas J. Watson Research Center)
This summer school will introduce graduate students to sketching-based approaches to computational linear and multi-linear algebra. Sketching here refers to a set of techniques for compressing a matrix, to one with fewer rows, or columns, or entries, usually via various kinds of random linear maps. We will discuss matrix computations, tensor algebras, and such sketching techniques, together with their applications and analysis.
Updated on Nov 03, 2022 11:59 AM PDT -
Summer Graduate School Concentration Inequalities and Localization Techniques in High Dimensional Probability and Geometry (SLMath)
Organizers: Max Fathi (Université Paris Cité), Dan Mikulincer (Massachusetts Institute of Technology)The goal of the summer school is for the students to first become familiar with the concept of concentration of measure in different settings (Euclidean, Riemannian and discrete), and the main open problems surrounding it. The students will later become familiar with the proof techniques that involve the different types of localization and obtain expertise on the ways to apply the localization techniques. After attending the graduate school, the students are expected to have the necessary background that would give them a chance to both conduct research around open problems in concentration of measure, find new applications to existing localization techniques and perhaps also develop new localization techniques.
Updated on Oct 20, 2023 09:42 AM PDT -
Summer Graduate School Machine Learning (UC San Diego)
Organizers: Ery Arias-Castro (University of California, San Diego), Mikhail Belkin (University of California, San Diego), Yusu Wang (Univ. California, San Diego), Lily Weng (University of California, San Diego)The overarching goal of this summer school is to expose the students both to modern forms of unsupervised learning — in the form of geometrical and topological data analysis — and to supervised learning — in the form of (deep) neural networks applied to regression/classification problems. The organizers have opted for a lighter exposure to a broader range of topics. Using the metaphor of a meal, we are offering 2 + 2 samplers — geometry and topology for data analysis + theoretical and practical deep learning — rather than 1 + 1 main dishes. The main goal, thus, is to inspire the students to learn more about one or several of the topics covered in the school.
The expected learning outcomes for students attending the school are the following:
1. An introduction to how concepts and tools from geometry and topology can be leveraged to perform data analysis in situations where the data are not labeled.
2. An introduction to recent and ongoing theoretical and methodological/practical developments in the use of neural networks for data analysis (deep learning).
Updated on Aug 29, 2023 11:59 AM PDT -
Summer Graduate School Introduction to Derived Algebraic Geometry (UC Berkeley)
Organizers: Benjamin Antieau (Northwestern University), Dmytro Arinkin (University of Wisconsin-Madison) Schur quartic x 4−xy3 = z 4−zu3 and several of the 64 lines that it contains
Schur quartic x 4−xy3 = z 4−zu3 and several of the 64 lines that it containsDerived algebraic geometry is an ‘update’ of algebraic geometry using ‘derived’ (roughly speaking, homological) techniques. This requires recasting the very foundations of the field: rings have to be replaced by differential graded algebras (or other forms of derived rings), categories by higher categories, and so on. The result is a powerful set of new tools, useful both within algebraic geometry and in related areas. The school serves as an introduction to these techniques, focusing on their applications.
The school is built around two related courses on geometric (‘derived spaces’) and categorical (‘derived categories’) aspects of the theory. Our goal is to explain the key ideas and concepts, while trying to keep technicalities to a minimum.
Updated on Jun 28, 2023 04:05 PM PDT -
Summer Graduate School Topics in Geometric Flows and Minimal Surfaces (St. Mary's College)
Organizers: Ailana Fraser (University of British Columbia), Lan-Hsuan Huang (University of Connecticut), Catherine Searle (Wichita State University), Lu Wang (Yale University) Soap bubble: equilibrium solution of the rescaled mean curvature flow and constant curvature surface.
Soap bubble: equilibrium solution of the rescaled mean curvature flow and constant curvature surface.This graduate summer school will introduce students to two important and inter-related fields of differential geometry: geometric flows and minimal surfaces.
Geometric flows have had far reaching influences on numerous branches of mathematics and other scientific disciplines. An outstanding example is the completion of Hamilton’s Ricci flow program by Perelman, leading to the resolution of the Poincare conjecture and Thurston’s geometrization conjecture for 3-manifolds. In this part of the summer school, students will be guided through basic topics and ideas in the study of geometric flows.
Since Penrose used variations of volume to formulate and study black holes in general relativity (in his Nobel prize-winning work), the intriguing connections between minimal surfaces and general relativity have been a strong driving force for the modern developments of both research areas. This part of the summer school will introduce students to the basic theory of minimal submanifolds and its applications in Riemannian geometry and general relativity.
The curriculum of this program will be accessible and will have a broad appeal to graduate students from a variety of mathematical areas, introducing some of the latest developments in each area and the remaining open problems therein, while simultaneously emphasizing their synergy.
Updated on Jun 29, 2023 10:56 AM PDT -
Summer Graduate School Mathematics and Computer Science of Market and Mechanism Design (SLMath)
Organizers: Yannai Gonczarowski (Harvard University), Irene Lo (Stanford University), Ran Shorrer (Pennsylvania State University), LEAD Inbal Talgam-Cohen (Technion---Israel Institute of Technology)
This school is associated with an upcoming research program at MSRI under the same title. The goal of the school is to equip students unfamiliar with these topics with the mathematical and theoretical computer science toolbox that forms the foundation of market and mechanism design.
Updated on Jun 28, 2023 01:19 PM PDT -
Summer Graduate School Séminaire de Mathématiques Supérieures 2023: Periodic and Ergodic Spectral Problems (Montréal, Canada)
Organizers: Alexander Elgart (Virginia Polytechnic Institute and State University), Vojkan Jaksic (McGill University), Svetlana Jitomirskaya (University of California, Irvine), Ilya Kachkovskiy (Michigan State University), Jean Lagacé (King's College London), Leonid Parnovski (University College London)This two week school will focus on spectral theory of periodic, almost-periodic, and random operators. The main aim of this school is to teach the students who work in one of these areas, methods used in parallel problems, explain the similarities between all these areas and show them the `big picture'.
Updated on Apr 06, 2023 06:24 PM PDT -
Summer Graduate School Algebraic Methods for Biochemical Reaction Networks (Leipzig, Germany)
Organizers: Timo de Wolff (TU Braunschweig), LEAD Alicia Dickenstein (University of Buenos Aires), Elisenda Feliu (University of Copenhagen) A basic enzymatic mechanism
A basic enzymatic mechanismThe aim of the course is to learn how tools from algebraic geometry (in particular, from computational and real algebraic geometry) can be used to analyze standard models in molecular biology. Particularly, these models are key ingredients in the development of Systems and Synthetic biology, two active research areas focusing on understanding, modifying, and implementing the design principles of living systems.
We will focus on the mathematical aspects of the methods, and exemplify and apply the theory to real networks, thereby introducing the participants to relevant problems and mechanisms in molecular biology. As a counterpart, however, the participants will also see how this field has in the past challenged current methods, mainly in the realm of real algebraic geometry, and has given rise to new general and purely theoretical results on polynomial equations. We will end our lectures with an overview of open questions in both fields.
Updated on Jun 15, 2023 08:39 AM PDT -
MSRI-UP MSRI-UP 2023: Topological Data Analysis
Organizers: Federico Ardila (San Francisco State University), LEAD Maria Mercedes Franco (Queensborough Community College (CUNY)), Rebecca Garcia (Colorado College), Jose Perea (Northeastern University), Candice Price (Smith College), Robin Wilson (Loyola Marymount University)The MSRI-UP summer program is designed to serve a diverse group of undergraduate students who would like to conduct research in the mathematical sciences.
In 2023, MSRI-UP will focus on Topological Data Analysis. The research program will be led by Dr. Jose Perea, Associate Professor in the Department of Mathematics and the Khoury College of Computer Sciences at Northeastern University.
Updated on Mar 07, 2024 12:48 PM PST -
Summer Graduate School Formalization of Mathematics (SLMath)
Organizers: Jeremy Avigad (Carnegie Mellon University), Heather Macbeth (Fordham University at Lincoln Center), Patrick Massot (Université Paris-Saclay) Some basic concepts in mathlib and the dependencies between them
Some basic concepts in mathlib and the dependencies between themComputational proof assistants now make it possible to develop global, digital mathematical libraries with theorems that are fully checked by computer. This summer school will introduce students to the new technology and the ideas behind it, and will encourage them to think about the goals and benefits of formalized mathematics. Students will learn to use the Lean interactive proof assistant, and by the end of the session they will be in a position to formalize mathematics on their own, join the Lean community, and contribute to its mathematical library.
Updated on Oct 20, 2023 10:07 AM PDT -
Summer Graduate School Commutative Algebra and its Interaction with Algebraic Geometry (Notre Dame)
Organizers: Steven Cutkosky (University of Missouri), LEAD Claudia Polini (University of Notre Dame), Claudiu Raicu (University of Notre Dame), Steven Sam (University of California, San Diego), Kevin Tucker (University of Illinois at Chicago)
Commutative Algebra has seen an extraordinary development in the last few years. Long standing conjectures have been proven and new connections to different areas of mathematics have been built.This summer graduate school will consist of three mini-courses (5 lectures each) on fundamental topics in commutative algebra that are not covered in the standard courses. Each course will be accompanied by problem sessions focused on research. Five general colloquium-style lectures will be given by invited scholars who will also attend the school and help with afternoon research activities.
Updated on Mar 20, 2023 01:33 PM PDT -
MAY-UP Mathematically Advancing Young Undergraduates Program (MAY-UP) [2023 Pilot Program]
Organizers: Duane Cooper (Morehouse College), Shelby Wilson (Johns Hopkins University Applied Physics Lab)2023 Pilot Program: The goal of MAY-UP is to provide students with a glimpse into Linear Algebra; and the ways in which this topic may arise both theoretically and computationally in their future studies. Material will include an introduction to matrices as well as basic matrix operations. We will also provide students with introductory programming skills in Python, including development environment setup and matrix manipulations via code.
Updated on Apr 18, 2024 06:03 AM PDT
