-
A Celebration for Women in Mathematics (2024) - May 12 Initiative
Organizers: Ini Adinya (University of Ibadan), Nasrin Altafi (Queen's University), Maria-Grazia Ascenzi (University of California Los Angeles), Shanna Dobson (University of California, Riverside), Malena Espanol (Arizona State University), Eleonore Faber (Karl-Franzens-Universität Graz; University of Leeds), Anna Fino (Università di Torino), Adi Glucksam (Northwestern University), Eloísa Grifo (University of Nebraska), Céleste Hogan (Texas Tech University), Ellen Kirkman (Wake Forest University), Kuei-Nuan Lin (Pennsylvania State University), Liangbing Luo (Lehigh University), LEAD Ornella Mattei (San Francisco State University), Claudia Miller (Syracuse University), Julia Plavnik (Indiana University), Claudia Polini (University of Notre Dame), Hema Srinivasan (University of Missouri), Špela Špenko (Université Libre de Bruxelles) "May 12 Initiative" Annual Workshop
"May 12 Initiative" Annual WorkshopThe Simons Laufer Mathematical Sciences Institute (SLMath) celebrates the "May 12 Initiative" with a panel discussion and social event open to all on the topic "Being a Woman in Mathematics". This is a hybrid event taking place on Zoom and in person at SLMath. This event is free and open to worldwide participation.
If you plan to participate online, please connect using this LINK.
Updated on May 03, 2024 01:11 PM PDT -
Macaulay2, Computational Algebraic Geometry and String Theory
Organizers: David Eisenbud (University of California, Berkeley), Daniel Grayson, Anton Leykin (Georgia Institute of Technology), Andre Lukas (University of Oxford), Devlin Mallory (University of Utah), Liam McAllister (Cornell University), Karl Schwede (University of Utah), Michael Stillman (Cornell University)Updated on Apr 11, 2024 01:36 PM PDT -
Connections Workshop: New Frontiers in Curvature & Special Geometric Structures and Analysis
Organizers: Sun-Yung Chang (Princeton University), Lan-Hsuan Huang (University of Connecticut), Chikako Mese (Johns Hopkins University), Ilaria Mondello (Université Paris-Est Créteil Val-de-Marne), LEAD Guofang Wei (University of California, Santa Barbara), LEAD Xuwen Zhu (Northeastern University) Geosurface
GeosurfaceThis three-day workshop will consist of various talks given by prominent female mathematicians on topics of differential geometry and geometric analysis. These will be appropriate for graduate students, post-docs, and researchers in areas related to the two programs. The workshop will also include activities to promote interaction and connection between participants. This workshop is open to all mathematicians.
Updated on Apr 30, 2024 11:01 AM PDT -
Introductory Workshop: New Frontiers in Curvature
Organizers: Ailana Fraser (University of British Columbia), Karsten Grove (University of Notre Dame), Richard Schoen (Stanford University), Catherine Searle (Wichita State University), LEAD Lu Wang (Yale University) The spatial Schwarzschild space with minimal surface boundary foliated by the inverse mean curvature flow
The spatial Schwarzschild space with minimal surface boundary foliated by the inverse mean curvature flowThis workshop will include introductory lectures on each of the four main topics of the program: geometric flows, geometric problems in mathematical relativity, global Riemannian geometry, and minimal submanifolds. The workshop will also have semi-expository lectures on recent advances and breakthroughs involving interactions between the four main topics. This will set the stage and provide important context for the semester-long program itself.
Updated on Apr 30, 2024 11:03 AM PDT -
Introductory Workshop: Special Geometric Structures and Analysis
Organizers: Anda Degeratu (Universität Stuttgart), LEAD Eleonora Di Nezza (Institut de Mathématiques de Jussieu), Luca Spolaor (University of California, San Diego), Song Sun (University of California, Berkeley)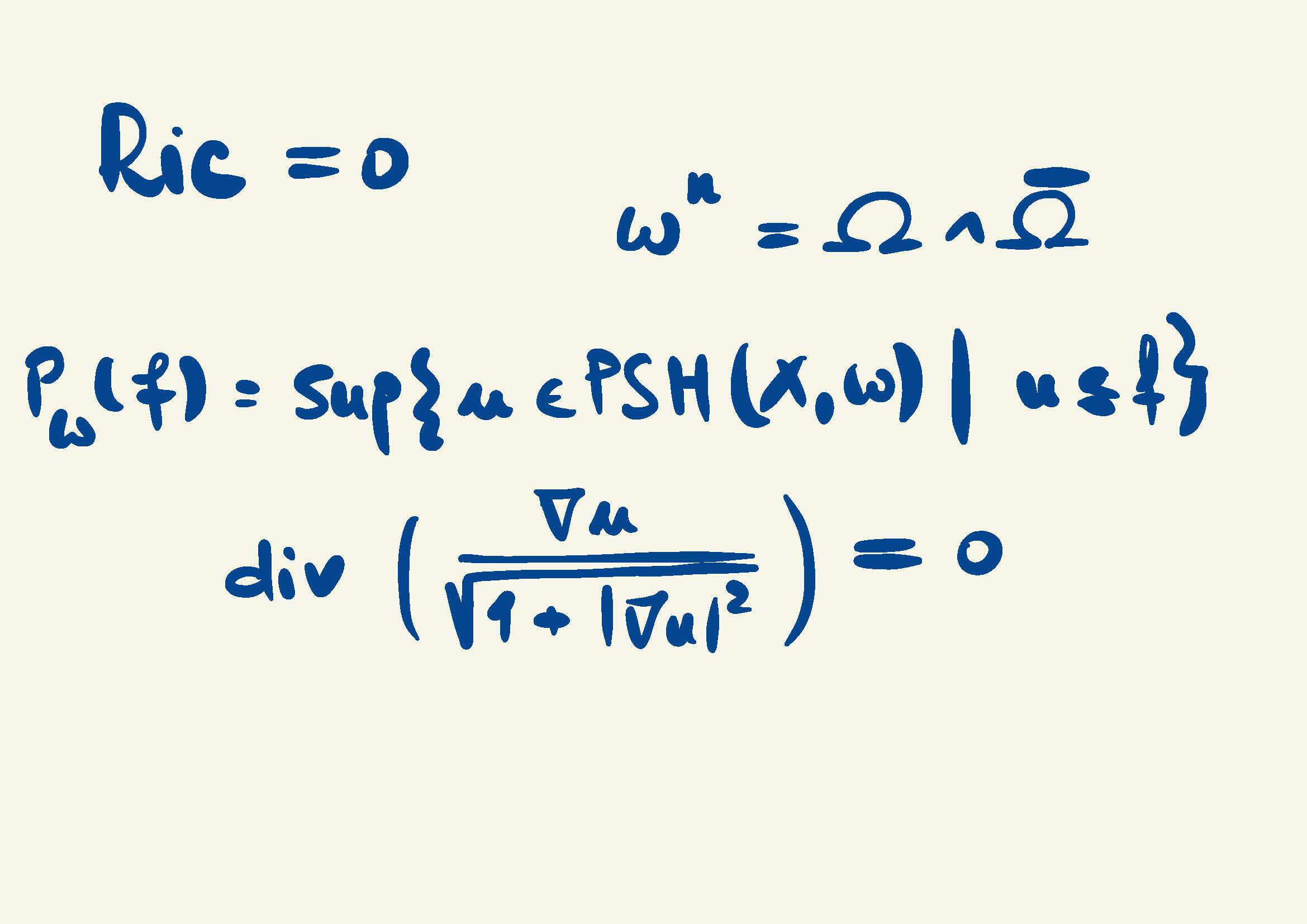
This workshop aims to prepare the participants for the main program: Special Geometric Structures and Analysis.
There will be introductory lectures to recent results in geometry and analysis; more precisely in Kähler geometry, special holonomy, microlocal analysis and geometric measure theoryUpdated on Apr 30, 2024 11:05 AM PDT -
Recent progress on geometric analysis and Riemannian geometry
Organizers: LEAD Lan-Hsuan Huang (University of Connecticut), Andre Neves (University of Chicago), Richard Schoen (Stanford University), LEAD Catherine Searle (Wichita State University), Guofang Wei (University of California, Santa Barbara) <p>The Hopf fibration of <span class="math-tex">\(S^3 \space by \space S^1\)</span></p>
<p>The Hopf fibration of <span class="math-tex">\(S^3 \space by \space S^1\)</span></p>This workshop will bring together researchers at the frontiers of geometric analysis and Riemannian geometry, with a focus on recent advances on geometric flows, geometric problems in mathematical relativity, global Riemannian geometry, and minimal submanifolds. These areas have shown highly intriguing interactions in recent years and we expect this workshop will provide a unique opportunity to facilitate these emerging links.
Updated on Apr 30, 2024 11:06 AM PDT -
Geometry and analysis of special structures on manifolds
Organizers: Anna Fino (Università di Torino), Mark Haskins (Duke University), Tristan Riviere (ETH Zurich), Neshan Wickramasekera (University of Cambridge)
The analysis of solutions to nonlinear geometric PDEs with higher-dimensional singular sets has seen some notable recent advances, but many fundamental questions still remain open. This workshop will bring together a wide array of researchers working in differential geometry, gauge theory, nonlinear PDEs, microlocal analysis, the calculus of variations and geometric measure theory, with the goal of describing recent advances, advertising recent technical breakthroughs and forging new connections.
Updated on Apr 30, 2024 11:08 AM PDT -
Hot Topics: Life after the Telescope Conjecture
Organizers: LEAD Agnes Beaudry (University of Colorado), Michael Hill (University of California, Los Angeles), Vesna Stojanoska (University of Illinois at Urbana-Champaign)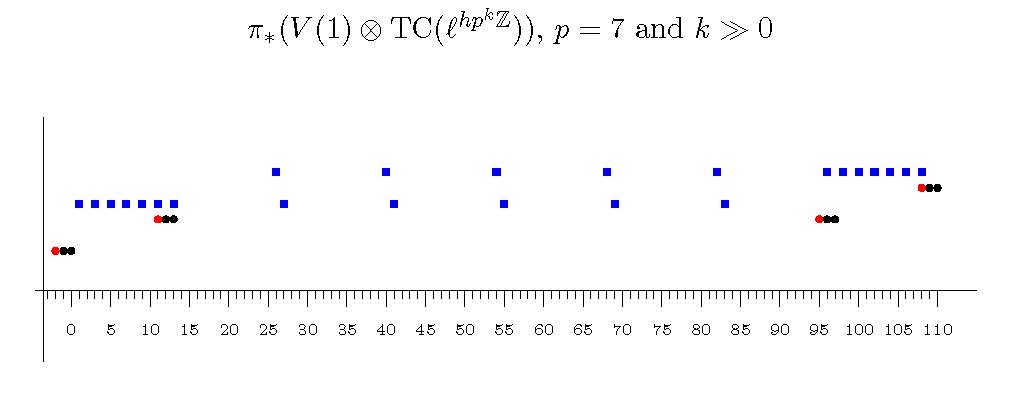
In June 2023, Burklund, Hahn, Levy, and Schlank surprised the homotopy theory community when they announced a disproof of Ravenel's Telescope Conjecture, a fundamental problem of homotopy theory which had been open for 40 years and was believed to be out of reach. The disproof of the Telescope Conjecture combines some of the most exciting recent developments in homotopy theory. This includes fundamental work on red-shift phenomena and descent in algebraic K-theory, trace methods based on a novel approach to topological Hochschild and cyclic homology, ambidexterity in chromatic homotopy theory, and more.
The workshop will explore this amazing body of work, culminating in its synthesis and ingenious application to disprove the Telescope Conjecture.
Updated on Apr 30, 2024 11:09 AM PDT -
Connections Workshop: Probability and Statistics of Discrete Structures
Organizers: Christina Goldschmidt (University of Oxford), Po-Ling Loh (University of Cambridge), Kavita Ramanan (Brown University), Dana Randall (Georgia Institute of Technology), LEAD Nike Sun (Massachusetts Institute of Technology) AI-generated interpretation of a random network
AI-generated interpretation of a random networkThis two-day workshop will bring together researchers from discrete mathematics, probability theory, theoretical computer science, and statistics to explore topics at their interface. The focus will be on probability and statistics of random discrete structures, as well as their applications, including in computer science and physical systems. The workshop will celebrate academic and gender diversity, bringing together women and men at junior and senior levels of their careers from mathematics, physics, and computer science.
Updated on May 30, 2023 03:32 PM PDT -
Introductory Workshop: Probability and Statistics of Discrete Structures
Organizers: Louigi Addario-Berry (McGill University), LEAD Shankar Bhamidi (University of North Carolina), Christina Goldschmidt (University of Oxford), Dana Randall (Georgia Institute of Technology), Perla Sousi (University of Cambridge), Remco van der Hofstad (Technische Universiteit Eindhoven) Visualization of a network constructed using simple probabilistic rules, showing the emergence of hubs and other macroscopic network phenomenon. From https://graph-tool.skewed.de
Visualization of a network constructed using simple probabilistic rules, showing the emergence of hubs and other macroscopic network phenomenon. From https://graph-tool.skewed.deNetworks, graph driven algorithms, and dynamics on graphs such as epidemics, random walks and centrality measures all play a major role, both in our daily lives as well as many scientific and engineering disciplines. This introductory workshop will bring together experts and junior researchers in combinatorics, probability, and statistics to share a broad vision of major challenges and objectives, with a primary focus on models of random graphs and their limits, network inference, dynamic processes on networks and algorithms and optimization on random structures.
Updated on May 30, 2023 11:38 AM PDT -
Connections Workshop: Extremal Combinatorics
Organizers: Julia Böttcher (London School of Economics and Political Science), Anita Liebenau (University of New South Wales), LEAD Maya Stein (Universidad de Chile)
The purpose of this workshop is to bring together promising early-career researchers in extremal combinatorics who are women or from underrepresented minorities so that they can meet with, forge connections with, and be inspired by the leading figures in the area. The workshop will include lectures, time for collaborative research, and an informal panel discussion session among female and minority researchers on career issues.
Updated on Apr 04, 2023 08:43 AM PDT -
Introductory Workshop - Graph Theory: Extremal, Probabilistic and Structural
Organizers: LEAD Penny Haxell (University of Waterloo), Michael Krivelevich (Tel Aviv University), Alex Scott (University of Oxford)
This workshop will feature leading experts in several major areas of graph theory, including extremal, probabilistic and structural aspects of the field. Introductory lectures will form an important part of the program, providing background and motivation, and aimed at a general mathematical audience. Complementing these, research talks will share exciting recent developments in graph theory.
Updated on Mar 31, 2023 03:48 PM PDT -
Hot Topics: Interactions between Harmonic Analysis, Homogeneous Dynamics, and Number Theory
Organizers: Dubi Kelmer (Boston College), LEAD Amir Mohammadi (University of California, San Diego), Hong Wang (New York University, Courant Institute)
In recent years techniques from harmonic analysis viz. projection theorems have found striking applications in finitary analysis on homogenous spaces. Such quantitative results have many potential applications to analytic number theory. This workshop will bring together researchers in these areas to further explore these connections.
Updated on Apr 12, 2024 09:01 AM PDT -
Algebraic and Analytic Methods in Combinatorics
Organizers: Janos Pach (Alfréd Rényi Institute of Mathematics), Andrew Suk (University of California, San Diego), LEAD Yufei Zhao (Massachusetts Institute of Technology) A degree 7 curve passing through 35 points in the plane
A degree 7 curve passing through 35 points in the planeMany exciting breakthroughs in combinatorics involve innovative applications of techniques from a wide range of areas such as harmonic analysis, polynomial and linear algebraic methods, spectral graph theory, and representation theory. This workshop will present recent developments in this area and facilitate discussions of research problems.
Updated on Jul 19, 2023 04:10 PM PDT -
Detection, Estimation, and Reconstruction in Networks
Organizers: Po-Ling Loh (University of Cambridge), Gabor Lugosi (ICREA), Sofia Olhede (École Polytechnique Fédérale de Lausanne (EPFL)), Roberto Oliveira (Institute of Pure and Applied Mathematics (IMPA)), LEAD Miklos Racz (Northwestern University) Recovering communities in a network.
Recovering communities in a network.In a growing number of applications, one needs to analyze and interpret data coming from massive networks. The statistical problems arising from such applications lead to important mathematical challenges: building novel probabilistic models, understanding the possibilities and limitations for statistical detection and inference, designing efficient algorithms, and understanding the inherent limitations of fast algorithms. The workshop will bring together leading researchers in combinatorial statistics, machine learning, and random graphs in the hope of cross-fertilization of ideas.
Updated on Aug 05, 2023 10:06 AM PDT
|
|
All upcoming workshops |
