-
Workshop A Celebration for Women in Mathematics (2024) - May 12 Initiative
Organizers: Ini Adinya (University of Ibadan), Nasrin Altafi (Queen's University), Maria-Grazia Ascenzi (University of California Los Angeles), Shanna Dobson (University of California, Riverside), Malena Espanol (Arizona State University), Eleonore Faber (Karl-Franzens-Universität Graz; University of Leeds), Anna Fino (Università di Torino), Adi Glucksam (Northwestern University), Eloísa Grifo (University of Nebraska), Céleste Hogan (Texas Tech University), Ellen Kirkman (Wake Forest University), Kuei-Nuan Lin (Pennsylvania State University), Liangbing Luo (Lehigh University), LEAD Ornella Mattei (San Francisco State University), Claudia Miller (Syracuse University), Julia Plavnik (Indiana University), Claudia Polini (University of Notre Dame), Hema Srinivasan (University of Missouri), Špela Špenko (Université Libre de Bruxelles) "May 12 Initiative" Annual Workshop
"May 12 Initiative" Annual WorkshopThe Simons Laufer Mathematical Sciences Institute (SLMath) celebrates the "May 12 Initiative" with a panel discussion and social event open to all on the topic "Being a Woman in Mathematics". This is a hybrid event taking place on Zoom and in person at SLMath. This event is free and open to worldwide participation - please register online for Zoom link & details.
Updated on Apr 23, 2024 09:42 AM PDT -
MAY-UP Mathematically Advancing Young Undergraduates Program (MAY-UP) 2024
Updated on Apr 26, 2024 08:45 AM PDT -
Summer Graduate School Séminaire de Mathématiques Supérieures 2024: Flows and Variational Methods in Riemannian and Complex Geometry: Classical and Modern Methods (Montréal, Canada)
Organizers: Vestislav Apostolov (Université du Québec à Montréal), Eleonora Di Nezza (Institut de Mathématiques de Jussieu), Pengfei Guan (McGill University), Spiro Karigiannis (University of Waterloo), Julien Keller (Université du Québec à Montréal), Alina Stancu (Concordia University), Valentino Tosatti (New York University, Courant Institute)
This school will present various developments in Riemannian and Kähler geometry around the notion of curvature seen as a tool to describe and understand the geometry of the objects. The school will give graduate students the opportunity to learn key ideas and techniques of the field, with an emphasis on solidifying foundations in view of potential future research. The first week will be centered around the question of the existence of Kähler metrics with special curvature properties and the famous Yau-Tian-Donaldson conjecture. The second week will focus on geometric flows in Riemannian and complex geometry.
Updated on Mar 18, 2024 02:15 PM PDT -
MSRI-UP MSRI-UP 2024: Mathematical Endocrinology
Organizers: Alexander Diaz-Lopez (Villanova University), Maria Mercedes Franco (Queensborough Community College (CUNY)), Rebecca Garcia (Colorado College), LEAD Candice Price (Smith College), Robin Wilson (Loyola Marymount University)The MSRI-UP summer program is designed to serve a diverse group of undergraduate students who would like to conduct research in the mathematical sciences.
In 2024, MSRI-UP will focus on Mathematical Endocrinology. The research program will be led by Dr. Erica J. Graham, Associate Professor in the Department of Mathematics at Bryn Mawr College.
Updated on Mar 07, 2024 11:11 AM PST -
Summer Graduate School Particle interactive systems: Analysis and computational methods (SLMath)
Organizers: LEAD Irene M. Gamba (University of Texas, Austin), Francois Golse (École Polytechnique), Qin Li (University of Wisconsin-Madison), Chiara Saffirio (Universität Basel)
This summer school will focus on the introductory notions related to the passage of Newtonian and quantum many-body dynamics to kinetic collisional models of Boltzmann flow models arising in statistical sciences in connection to model reductions when continuum macro dynamics arises; and their numerical schemes associated to transport of kinetic processes in classical and data driven mean field dynamics incorporating recent tools from computational kinetics and data science tools. There will be two sets of lectures: “From Newton to Boltzmann to Fluid dynamics”, and “Kinetic collisional theory in mean field regimes: analysis, discrete approximations, and applications”. Each lecture series will be accompanied by a collaboration session, led by the lecturer and teaching assistants. The purpose of the collaboration sessions is to encourage and strengthen higher-level thinking of the materials taught in the lectures and to direct further reading for interested students. Interactive learning activities will be conducted. For example, students will be given problem sets associated with the lectures and will work in small groups to discuss concepts and/or find solutions to assigned problems. The students will also be encouraged to give oral or poster presentations on their solutions or other materials relevant to the course.
Updated on Apr 10, 2024 02:59 PM PDT -
Summer Graduate School Special Geometric Structures and Analysis (St. Mary's College)
Organizers: Costante Bellettini (University College London), LEAD Eleonora Di Nezza (Institut de Mathématiques de Jussieu), Song Sun (University of California, Berkeley) a Calabi-Yau manifold
a Calabi-Yau manifoldThis summer school will serve as an introduction to the SLMath program "Special geometric structures and analysis". There will be two mini-courses: one in Geometric Measure theory and the other in Microlocal Analysis. The aim is to give the basic notions of two subjects also treated during the program.
Updated on Apr 05, 2024 09:40 PM PDT -
Summer Graduate School Introduction to Quantum-Safe Cryptography (IBM Zurich)
Organizers: Jonathan Bootle (IBM Zürich Research Laboratory), Luca De Feo (IBM Zürich Research Laboratory)
This two week summer school, jointly organized by SLMath with IBM Zurich, will introduce students to the mathematics and algorithms used in the design and analysis of quantum-safe cryptosystems. Each week will be dedicated to two of the four families of quantum-safe schemes.
Updated on Apr 16, 2024 03:42 PM PDT -
Summer Graduate School H-principle (Sendai, Japan)
Organizers: Emmy Murphy (Princeton University), Takashi Tsuboi (RIKEN Interdisciplinary Theoretical and Mathematical Sciences Program) The image of a large sphere isometrically embedded into a small space through a C^1 embedding. (Attributions: E. Bartzos, V. Borrelli, R. Denis, F. Lazarus, D. Rohmer, B. Thibert)
The image of a large sphere isometrically embedded into a small space through a C^1 embedding. (Attributions: E. Bartzos, V. Borrelli, R. Denis, F. Lazarus, D. Rohmer, B. Thibert)This two week summer school, jointly organized by SLMath with RIKEN, will introduce graduate students to the theory of h-principles. After building up the theory from basic smooth topology, we will focus on more recent developments of the theory, particularly applications to symplectic and contact geometry, fluid dynamics, and foliation theory.
h-principles in smooth topology (Emmy Murphy)
Riemannian geometry and applications to fluid dynamics (Dominik Inauen)
Contact and symplectic flexibility (Emmy Murphy)
Foliation theory and diffeomorphism groups (Takashi Tsuboi)Updated on Apr 17, 2024 10:55 AM PDT -
Summer Graduate School Stochastic Quantization (SLMath)
Organizers: Massimiliano Gubinelli (University of Oxford), Martina Hofmanova (Universität Bielefeld), LEAD Hao Shen (University of Wisconsin-Madison), Lorenzo Zambotti (Sorbonne Université)
This summer school will familiarize students with the basic problems of the mathematical theory of Euclidean quantum fields. The lectures will introduce some of its prominent models and analyze them via the so called “stochastic quantization” methods, involving recently developed stochastic and PDE techniques. This is an area which is highly interdisciplinary combining ideas ranging from the theory of partial differential equations, to stochastic analysis, to mathematical physics. Our goal is to bring together students who are perhaps familiar with some but not all of these subjects and teach them how to integrate these different tools to solve cutting-edge problems of Euclidean quantum field theory.
Updated on Apr 24, 2024 03:23 PM PDT -
Summer Graduate School Koszul Duality in the Local Langlands Program (St. Mary's College)
Organizers: Clifton Cunningham (University of Calgary), LEAD Sarah Dijols (University of Calgary)
This summer school provides the mathematical background to recognize Koszul duality in representation theory. The school is especially oriented toward applications in the local Langlands program, with an emphasis on real groups. As Koszul duality patterns have been initially observed in the context of Hecke algebras, our school will also introduce the students to Hecke algebras and their categorifications.
Updated on Apr 12, 2024 11:27 PM PDT -
Summer Graduate School Introduction to the Theory of Algebraic Curves (UC Berkeley)
Organizers: Izzet Coskun (University of Illinois, Chicago), Eric Larson (Brown University), LEAD Hannah Larson (University of California, Berkeley), Isabel Vogt (Brown University)
In the last few years, there have been extraordinary developments in many aspects of curve theory. Beginning with many examples in low genus, this summer school will introduce the participants to the background behind these developments in the following areas:
- moduli spaces of stable curves
- Brill–Noether theory
- the extrinsic geometry of the curves in projective space
We will also include an introduction to some open problems at the forefront of these active areas.
Updated on Apr 19, 2024 10:16 AM PDT -
Summer Graduate School Mathematics of General Relativity and Fluids (FORTH, Greece)
Organizers: LEAD Mihalis Dafermos (Princeton University), Grigorios Fournodavlos (University of Crete), Juhi Jang (University of Southern California), Igor Rodnianski (Princeton University) ALCF Visualization and Data Analytics Team; Adam Burrows and the Princeton Supernova Theory Group, Princeton University
ALCF Visualization and Data Analytics Team; Adam Burrows and the Princeton Supernova Theory Group, Princeton UniversityThis summer school will give an accessible introduction to the mathematical study of general relativity, a field which in the past has had barriers to entry due to its interdisciplinary nature, and whose study has been concentrated at specific institutions, to a wider audience of students studying at institutions throughout the U.S., Europe and Greece. Another goal of the summer school will be to demonstrate the common underlying mathematical themes in many problems which traditionally have been studied by separate research communities.
Updated on Mar 19, 2024 04:24 PM PDT -
Summer Graduate School Analysis of Partial Differential Equations (Okinawa Institute of Science and Technology)
Organizers: Ugur Abdulla (Okinawa Institute of Science and Technology), Gui-Qiang Chen (University of Oxford)This two week summer school, jointly organized by SLMath with OIST, will offer the following two mini-courses:
- Measure-theoretical analysis, divergence-measure fields, and nonlinear PDEs of divergence form
This course will present some recent developments in the theory of divergence-measure fields via measure-theoretic analysis and its applications to the analysis of nonlinear PDEs of conservative form – nonlinear conservation laws. - Perron’s method and Wiener-type criteria in the potential theory of elliptic and parabolic PDEs
This course will present some recent developments precisely characterizing the regularity of the point at ∞ for second order elliptic and parabolic PDEs and broadly extending the role of the Wiener test in classical analysis.
Updated on Apr 19, 2024 12:54 PM PDT - Measure-theoretical analysis, divergence-measure fields, and nonlinear PDEs of divergence form
-
Summer Graduate School Mathematical Spin Glass Theory (Courant, NY)
Organizers: Antonio Auffinger (Northwestern University), Wei-Kuo Chen (University of Minnesota), LEAD Eliran Subag (Weizmann Institute of Science)
While their original aim was to explain the strange behavior of certain magnetic alloys, the study of spin glass models has led to a far-reaching and beautiful physical theory whose techniques have been applied to a myriad of problems in theoretical computer science, statistics, optimization and biology. As many of the physical predictions can be formulated as purely mathematical questions, often extremely hard, about large random systems in high dimensions, in recent decades a new area of research has emerged in probability theory around these problems.
Mathematically, a mean-field spin glass model is a Gaussian process (random function) on the discrete hypercube or the sphere in high dimensions. A fundamental challenge in their analysis is, roughly speaking, to understand the size and structure of their super-level sets as the dimension tends to infinity, which are often studied through smooth objects like the free energy and Gibbs measure whose origin is in statistical physics. The aim of the summer school is to introduce students to landmark results on the latter while emphasizing the techniques and ideas that were developed to obtain them, as well as exposing the students to some recent research topics.
Updated on Apr 19, 2024 03:00 PM PDT -
Summer Graduate School Statistical Optimal Transport (St. Mary's College)
Organizers: LEAD Promit Ghosal (Brandeis University), Jonathan Niles-Weed (New York University, Courant Institute), Marcel Nutz (Columbia University)
This summer school offers an exceptional opportunity for participants to delve into the intricate realm of statistical optimal transport theory. This captivating field stands at the crossroads of multiple disciplines, drawing from a rich tapestry of mathematical insights from diverse subjects, including partial differential equations, stochastic analysis, convex geometry, statistics, and machine learning, crafting a vibrant and interdisciplinary landscape. The foremost objective of this summer school is to create a dynamic learning environment that unites students from diverse backgrounds such as PDE theory, probability, or optimal transport.
Updated on Mar 20, 2024 02:04 PM PDT -
Summer Graduate School Noncommutative Algebraic Geometry
Organizers: Pieter Belmans (University of Luxembourg), Lander Hermans (Universiteit Antwerp), Wendy Lowen (Universiteit Antwerpen), Arne Mertens (Universiteit Antwerp), Michel VAN DEN BERGH (Hasselt University), Špela Špenko (Université Libre de Bruxelles)Created on Apr 03, 2024 05:26 PM PDT -
Summer Graduate School Computer Assisted Proofs in Applied Mathematics (SLMath)
Organizers: LEAD Jonathan Jaquette (New Jersey Institute of Technology), Evelyn Sander (George Mason University)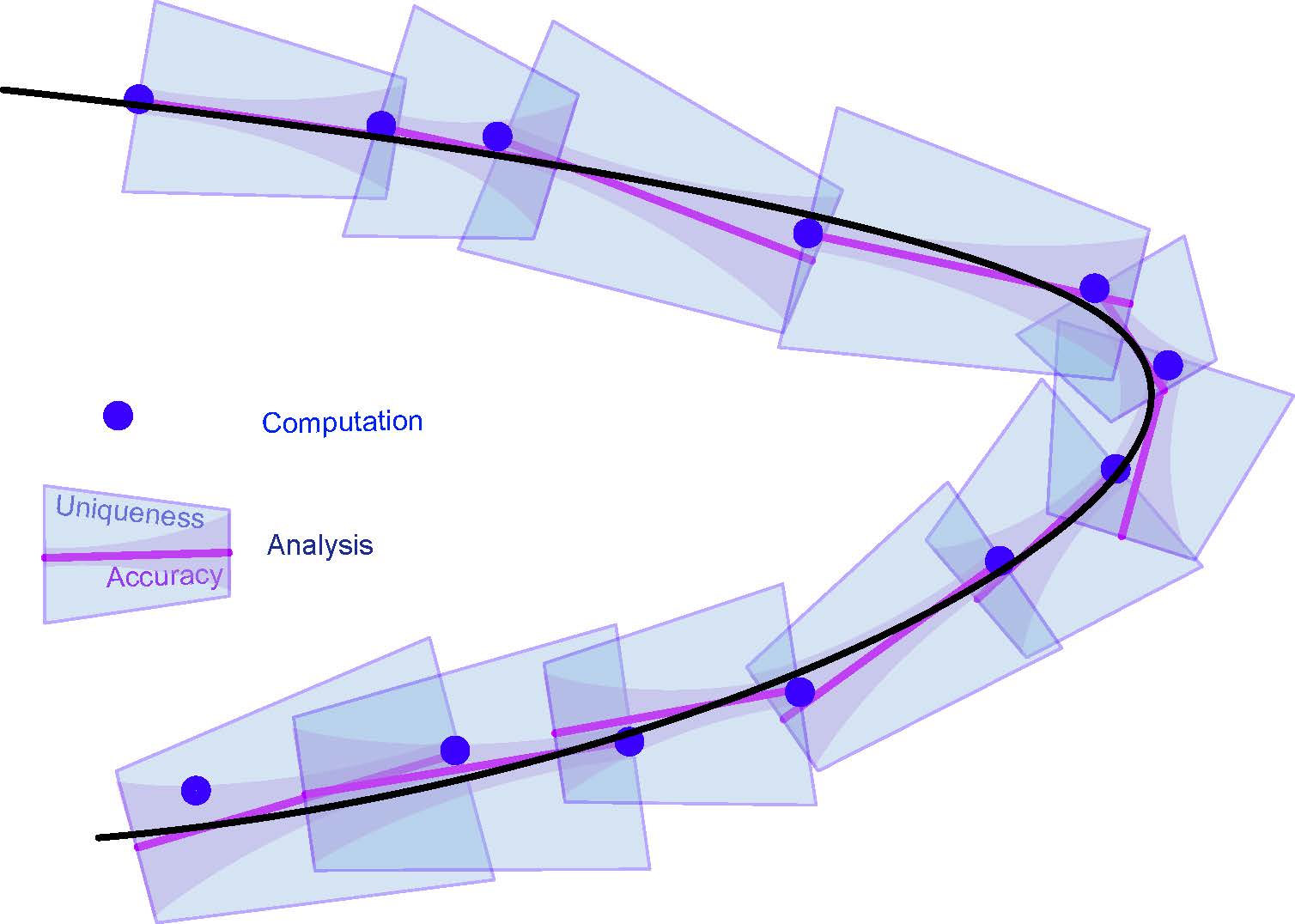
One of the core elements of applied mathematics is mathematical modeling consisting of nonlinear equations such as ODEs, and PDEs. A fundamental difficulty which arises is that most nonlinear models cannot be solved in closed form. Computer assisted proofs are at the forefront of modern mathematics and have led to many important recent mathematical advances. They provide a way of melding analytical techniques with numerical methods, in order to provide rigorous statements for mathematical models that could not be treated by either method alone. In this summer school, students will review standard computational and analytical techniques, learn to combine these techniques with more specialized methods of interval arithmetic, and apply these methods to establish rigorous results in otherwise intractable problems
Updated on Apr 08, 2024 08:55 AM PDT -
Summer Graduate School Geometry and Dynamics in Higher Rank Lie Groups (St. Mary's College)
Organizers: Richard Canary (University of Michigan), Sara Maloni (University of Virginia), Wenyu Pan (University of Toronto), Cagri Sert (University of Zurich), LEAD Tengren Zhang (National University of Singapore)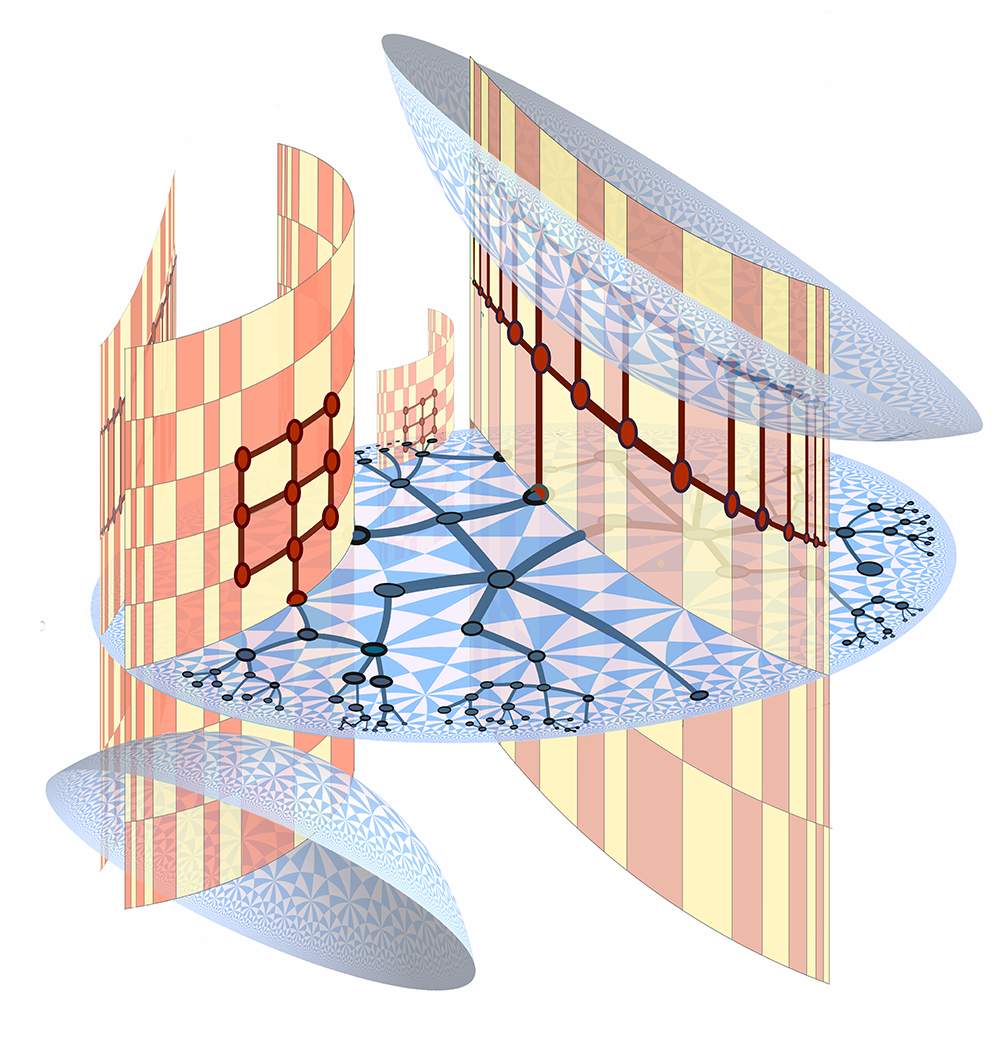 <p>Flats and hyperbolic planes in a higher rank symmetric space</p> Drawn by Steve Trettel.
<p>Flats and hyperbolic planes in a higher rank symmetric space</p> Drawn by Steve Trettel.Lie groups are central objects in modern mathematics; they arise as the automorphism groups of many homogeneous spaces, such as flag manifolds and Riemannian symmetric spaces. Often, one can construct manifolds locally modelled on these homogeneous spaces by taking quotients of their subsets by discrete subgroups of their automorphism groups. Studying such discrete subgroups of Lie groups is an active and growing area of mathematical research. The objective of this summer school is to introduce young researchers to a class of discrete subgroups of Lie groups, called Anosov subgroups.
Updated on Apr 18, 2024 08:43 AM PDT -
Summer Graduate School Topological and Geometric Structures in Low Dimensions (SLMath)
Organizers: LEAD Kenneth Bromberg (University of Utah), Kathryn Mann (Cornell University) <p>Laminations arise naturally in hyperbolic geometry and (pseudo-) Anosov flows [Image by Jeffrey Brock]</p>
<p>Laminations arise naturally in hyperbolic geometry and (pseudo-) Anosov flows [Image by Jeffrey Brock]</p>This school will serve as an introduction to the SLMath semester “Topological and Geometric Structures in Low-Dimensions”. The school consists of two mini-courses: one on Teichmüller Theory and Hyperbolic 3-Manifolds and the other on Anosov Flows on Geometric 3-Manifolds. Both topics lie at the interface of low-dimensional geometric topology (specifically, surfaces, foliations, and 3-manifolds) and low-dimensional dynamics. The first course will be targeted towards students who have completed the standard first year graduate courses in geometry, topology, and analysis while the second course will geared towards more advanced students who are closer to beginning research. However, we expect that all students will benefit from both courses.
Updated on Mar 21, 2024 09:48 AM PDT
Past Educational Events
-
Workshop Critical Issues in Mathematics Education 2024: Bringing Innovation to Scale: Teaching-Focused Faculty as Change Agents
Organizers: Debra Carney (Colorado School of Mines), Dave Kung (St. Mary's College of Maryland), P. Gavin LaRose (University of Michigan), Mary Pilgrim (San Diego State University), Chris Rasmussen (San Diego State University), Natasha Speer (University of Maine), Cristina Villalobos (University of Texas Rio Grande Valley)
The undergraduate mathematics education system remains a huge barrier to college completion and to equity in higher education. The problem in entry level mathematics courses is not a lack of innovation. Numerous projects and institutions have created, piloted, and occasionally replicated effective reform efforts that overcame particular challenges, like the need to improve pedagogical practices or attend to gender equity. The biggest barrier to systemic reform – implementing many of these research-backed innovations at scale – is a structural one, particularly at large research-focused institutions. This workshop will bring together a group of stakeholders to explore a new avenue for change, the rise of teaching-focused faculty at research-intensive institutions who increasingly influence introductory coursework. By creating a network that connects these faculty across institutions, change at scale across 50, 100, or even more institutions becomes possible – on issues ranging from pedagogy to equity to curricular innovation. Creating such structures would also allow for bringing future innovations to scale much more quickly than is currently possible.
Updated on Apr 19, 2024 06:56 AM PDT -
Workshop Hot Topics: MIP* = RE and the Connes’ Embedding Problem
Organizers: Michael Chapman (New York University, Courant Institute), Anand Natarajan (Massachusetts Institute of Technology), William Slofstra (University of Waterloo), John Wright (University of Texas, Austin), Henry Yuen (Columbia University)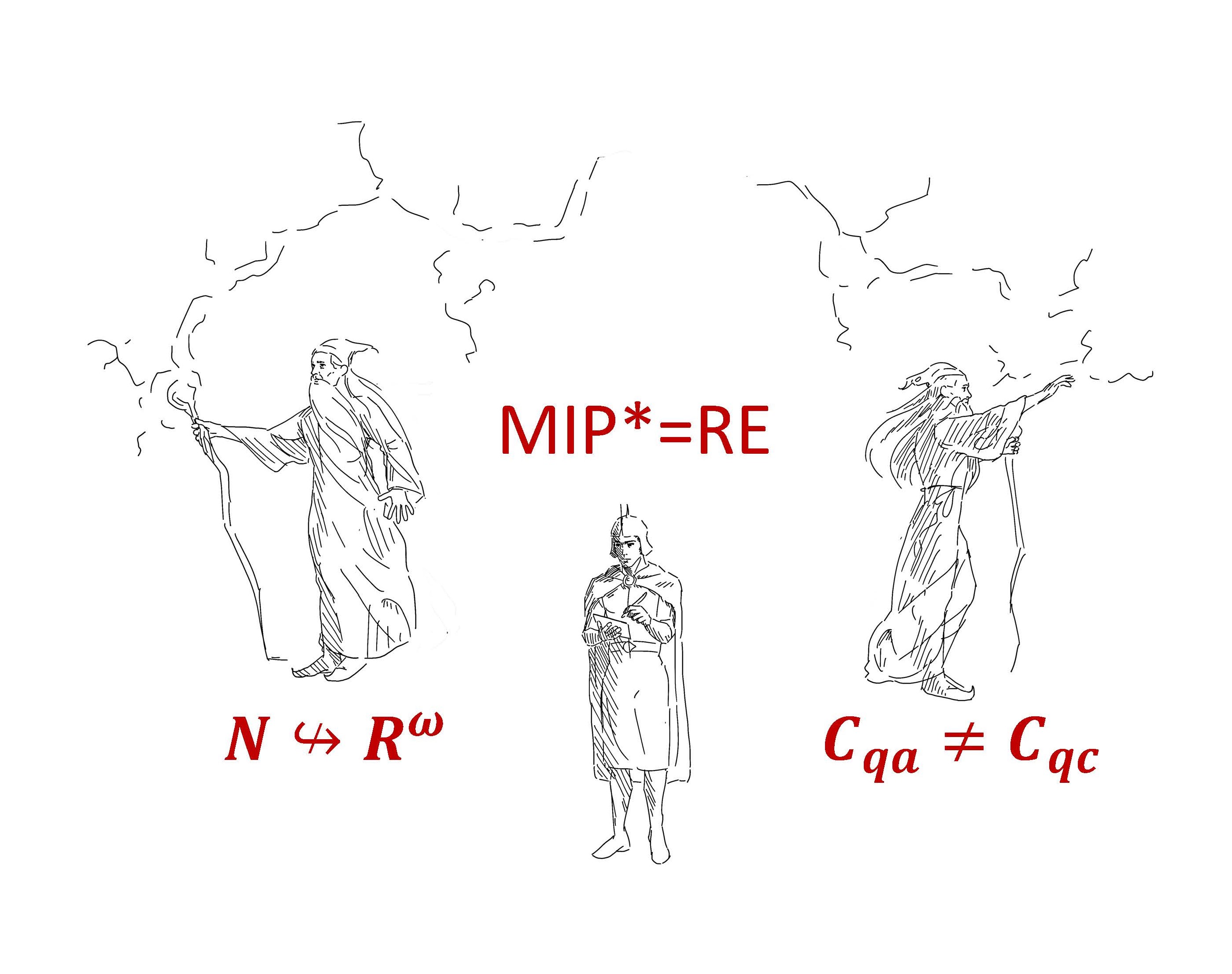 Drawing by Tina Zhang.
Drawing by Tina Zhang.This workshop is about the recent MIP*=RE result from quantum computational complexity, and the resulting resolution of the Connes embedding problem from the theory of von Neumann algebras. MIP*=RE connects the disparate areas of computational complexity theory, quantum information, operator algebras, and approximate representation theory. The aim of this workshop is to bridge this divide, by giving an in-depth exposition of the techniques used in the proof of MIP*=RE, and highlighting perspectives on the MIP*=RE result from operator algebras and approximate representation theory. In particular, this workshop will highlight connections with group stability, something that has not been covered in previous workshops. In addition to increasing understanding of the MIP*=RE proof, we hope that this will open up further applications of the ideas behind MIP*=RE in operator algebras.
Updated on Oct 25, 2023 11:46 AM PDT -
Summer Graduate School Foundations and Frontiers of Probabilistic Proofs (Zürich, Switzerland)
Organizers: Alessandro Chiesa (École Polytechnique Fédérale de Lausanne (EPFL))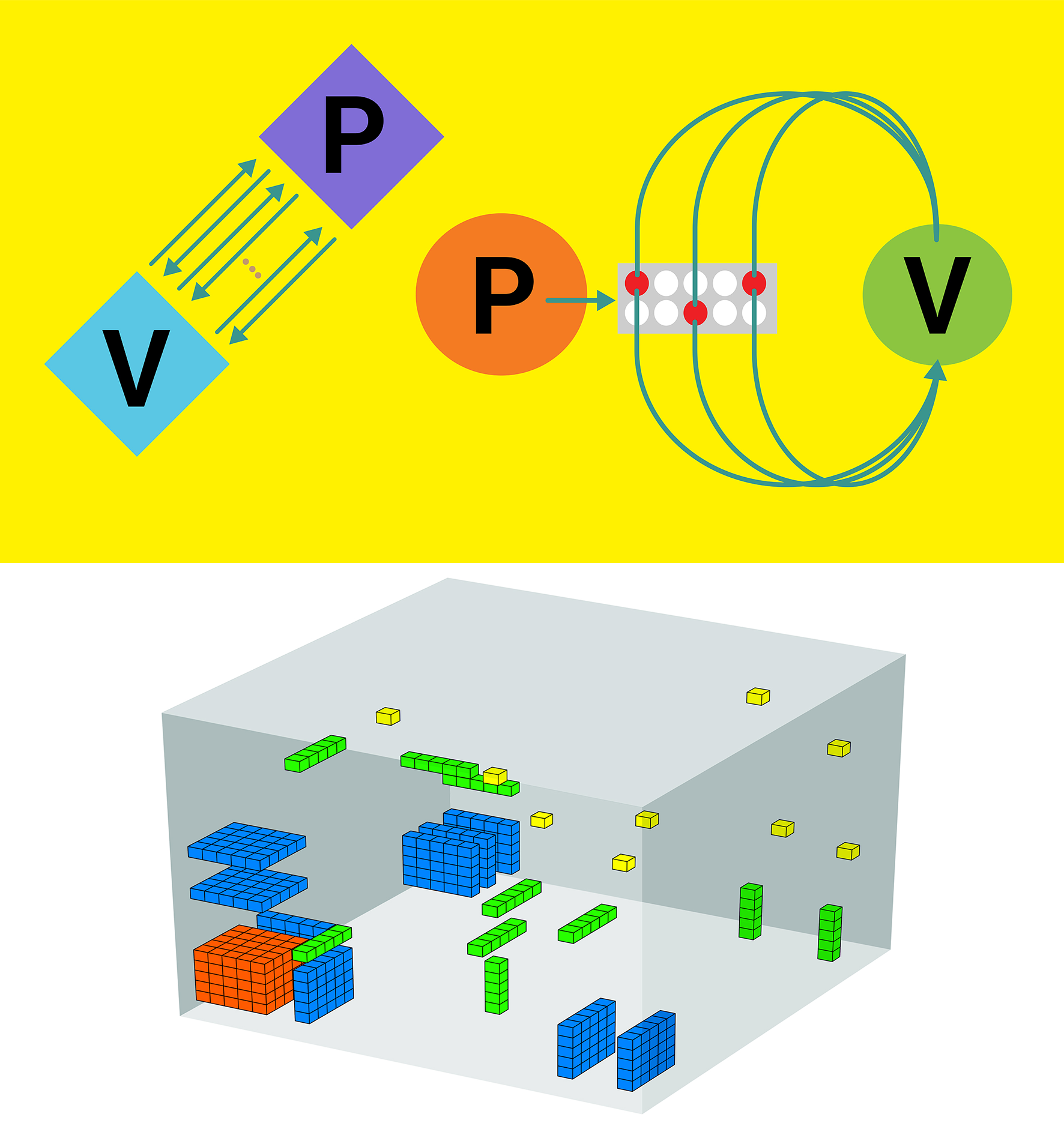 Several executions of a 3-dimensional sumcheck protocol with a random order of directions (thanks to Dev Ojha for creating the diagram)
Several executions of a 3-dimensional sumcheck protocol with a random order of directions (thanks to Dev Ojha for creating the diagram)Proofs are at the foundations of mathematics. Viewed through the lens of theoretical computer science, verifying the correctness of a mathematical proof is a fundamental computational task. Indeed, the P versus NP problem, which deals precisely with the complexity of proof verification, is one of the most important open problems in all of mathematics.
The complexity-theoretic study of proof verification has led to exciting reenvisionings of mathematical proofs. For example, probabilistically checkable proofs (PCPs) admit local-to-global structure that allows verifying a proof by reading only a minuscule portion of it. As another example, interactive proofs allow for verification via a conversation between a prover and a verifier, instead of the traditional static sequence of logical statements. The study of such proof systems has drawn upon deep mathematical tools to derive numerous applications to the theory of computation and beyond.
In recent years, such probabilistic proofs received much attention due to a new motivation, delegation of computation, which is the emphasis of this summer school. This paradigm admits ultra-fast protocols that allow one party to check the correctness of the computation performed by another, untrusted, party. These protocols have even been realized within recently-deployed technology, for example, as part of cryptographic constructions known as succinct non-interactive arguments of knowledge (SNARKs).
This summer school will provide an introduction to the field of probabilistic proofs and the beautiful mathematics behind it, as well as prepare students for conducting cutting-edge research in this area.
Updated on Oct 20, 2023 01:17 PM PDT -
Summer Graduate School Mathematics of Big Data: Sketching and (Multi-) Linear Algebra (IBM Almaden)
Organizers: Kenneth Clarkson (IBM Research Division), Lior Horesh (IBM Thomas J. Watson Research Center), Misha Kilmer (Tufts University), Tamara Kolda (MathSci.ai), Shashanka Ubaru (IBM Thomas J. Watson Research Center)
This summer school will introduce graduate students to sketching-based approaches to computational linear and multi-linear algebra. Sketching here refers to a set of techniques for compressing a matrix, to one with fewer rows, or columns, or entries, usually via various kinds of random linear maps. We will discuss matrix computations, tensor algebras, and such sketching techniques, together with their applications and analysis.
Updated on Nov 03, 2022 11:59 AM PDT -
Summer Graduate School Concentration Inequalities and Localization Techniques in High Dimensional Probability and Geometry (SLMath)
Organizers: Max Fathi (Université Paris Cité), Dan Mikulincer (Massachusetts Institute of Technology)The goal of the summer school is for the students to first become familiar with the concept of concentration of measure in different settings (Euclidean, Riemannian and discrete), and the main open problems surrounding it. The students will later become familiar with the proof techniques that involve the different types of localization and obtain expertise on the ways to apply the localization techniques. After attending the graduate school, the students are expected to have the necessary background that would give them a chance to both conduct research around open problems in concentration of measure, find new applications to existing localization techniques and perhaps also develop new localization techniques.
Updated on Oct 20, 2023 09:42 AM PDT -
Summer Graduate School Machine Learning (UC San Diego)
Organizers: Ery Arias-Castro (University of California, San Diego), Mikhail Belkin (University of California, San Diego), Yusu Wang (Univ. California, San Diego), Lily Weng (University of California, San Diego)The overarching goal of this summer school is to expose the students both to modern forms of unsupervised learning — in the form of geometrical and topological data analysis — and to supervised learning — in the form of (deep) neural networks applied to regression/classification problems. The organizers have opted for a lighter exposure to a broader range of topics. Using the metaphor of a meal, we are offering 2 + 2 samplers — geometry and topology for data analysis + theoretical and practical deep learning — rather than 1 + 1 main dishes. The main goal, thus, is to inspire the students to learn more about one or several of the topics covered in the school.
The expected learning outcomes for students attending the school are the following:
1. An introduction to how concepts and tools from geometry and topology can be leveraged to perform data analysis in situations where the data are not labeled.
2. An introduction to recent and ongoing theoretical and methodological/practical developments in the use of neural networks for data analysis (deep learning).
Updated on Aug 29, 2023 11:59 AM PDT -
Summer Graduate School Introduction to Derived Algebraic Geometry (UC Berkeley)
Organizers: Benjamin Antieau (Northwestern University), Dmytro Arinkin (University of Wisconsin-Madison)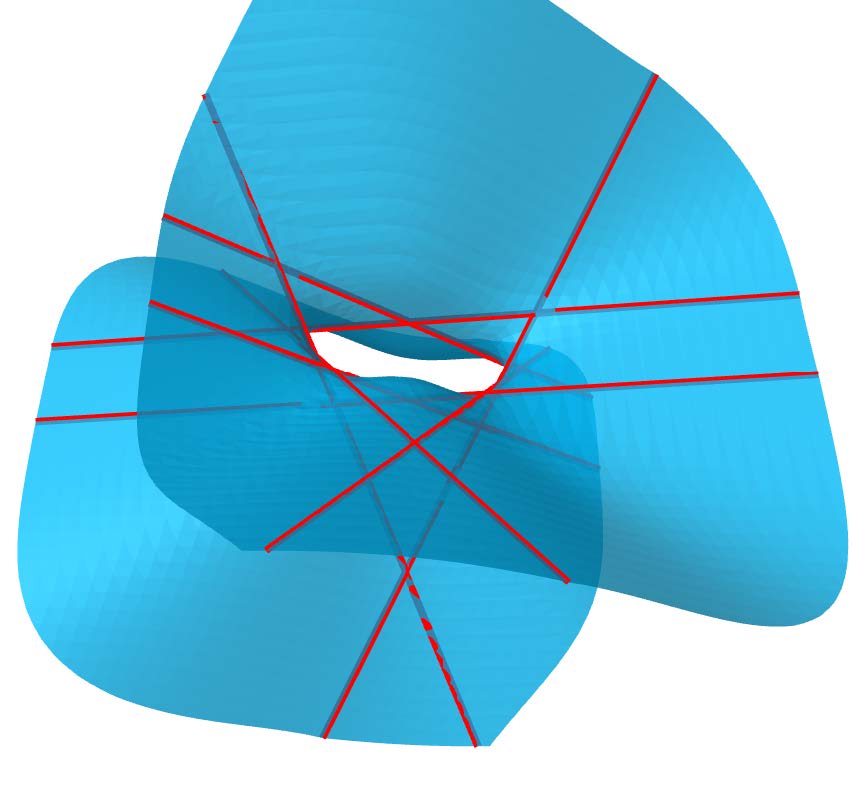 Schur quartic x 4−xy3 = z 4−zu3 and several of the 64 lines that it contains
Schur quartic x 4−xy3 = z 4−zu3 and several of the 64 lines that it containsDerived algebraic geometry is an ‘update’ of algebraic geometry using ‘derived’ (roughly speaking, homological) techniques. This requires recasting the very foundations of the field: rings have to be replaced by differential graded algebras (or other forms of derived rings), categories by higher categories, and so on. The result is a powerful set of new tools, useful both within algebraic geometry and in related areas. The school serves as an introduction to these techniques, focusing on their applications.
The school is built around two related courses on geometric (‘derived spaces’) and categorical (‘derived categories’) aspects of the theory. Our goal is to explain the key ideas and concepts, while trying to keep technicalities to a minimum.
Updated on Jun 28, 2023 04:05 PM PDT -
Summer Graduate School Topics in Geometric Flows and Minimal Surfaces (St. Mary's College)
Organizers: Ailana Fraser (University of British Columbia), Lan-Hsuan Huang (University of Connecticut), Catherine Searle (Wichita State University), Lu Wang (Yale University) Soap bubble: equilibrium solution of the rescaled mean curvature flow and constant curvature surface.
Soap bubble: equilibrium solution of the rescaled mean curvature flow and constant curvature surface.This graduate summer school will introduce students to two important and inter-related fields of differential geometry: geometric flows and minimal surfaces.
Geometric flows have had far reaching influences on numerous branches of mathematics and other scientific disciplines. An outstanding example is the completion of Hamilton’s Ricci flow program by Perelman, leading to the resolution of the Poincare conjecture and Thurston’s geometrization conjecture for 3-manifolds. In this part of the summer school, students will be guided through basic topics and ideas in the study of geometric flows.
Since Penrose used variations of volume to formulate and study black holes in general relativity (in his Nobel prize-winning work), the intriguing connections between minimal surfaces and general relativity have been a strong driving force for the modern developments of both research areas. This part of the summer school will introduce students to the basic theory of minimal submanifolds and its applications in Riemannian geometry and general relativity.
The curriculum of this program will be accessible and will have a broad appeal to graduate students from a variety of mathematical areas, introducing some of the latest developments in each area and the remaining open problems therein, while simultaneously emphasizing their synergy.
Updated on Jun 29, 2023 10:56 AM PDT -
Summer Graduate School Séminaire de Mathématiques Supérieures 2023: Periodic and Ergodic Spectral Problems (Montréal, Canada)
Organizers: Alexander Elgart (Virginia Polytechnic Institute and State University), Vojkan Jaksic (McGill University), Svetlana Jitomirskaya (University of California, Irvine), Ilya Kachkovskiy (Michigan State University), Jean Lagacé (King's College London), Leonid Parnovski (University College London)This two week school will focus on spectral theory of periodic, almost-periodic, and random operators. The main aim of this school is to teach the students who work in one of these areas, methods used in parallel problems, explain the similarities between all these areas and show them the `big picture'.
Updated on Apr 06, 2023 06:24 PM PDT -
Summer Graduate School Mathematics and Computer Science of Market and Mechanism Design (SLMath)
Organizers: Yannai Gonczarowski (Harvard University), Irene Lo (Stanford University), Ran Shorrer (Pennsylvania State University), LEAD Inbal Talgam-Cohen (Technion---Israel Institute of Technology)
This school is associated with an upcoming research program at MSRI under the same title. The goal of the school is to equip students unfamiliar with these topics with the mathematical and theoretical computer science toolbox that forms the foundation of market and mechanism design.
Updated on Jun 28, 2023 01:19 PM PDT -
Summer Graduate School Algebraic Methods for Biochemical Reaction Networks (Leipzig, Germany)
Organizers: Timo de Wolff (TU Braunschweig), LEAD Alicia Dickenstein (University of Buenos Aires), Elisenda Feliu (University of Copenhagen)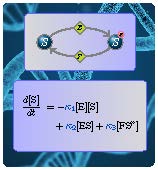 A basic enzymatic mechanism
A basic enzymatic mechanismThe aim of the course is to learn how tools from algebraic geometry (in particular, from computational and real algebraic geometry) can be used to analyze standard models in molecular biology. Particularly, these models are key ingredients in the development of Systems and Synthetic biology, two active research areas focusing on understanding, modifying, and implementing the design principles of living systems.
We will focus on the mathematical aspects of the methods, and exemplify and apply the theory to real networks, thereby introducing the participants to relevant problems and mechanisms in molecular biology. As a counterpart, however, the participants will also see how this field has in the past challenged current methods, mainly in the realm of real algebraic geometry, and has given rise to new general and purely theoretical results on polynomial equations. We will end our lectures with an overview of open questions in both fields.
Updated on Jun 15, 2023 08:39 AM PDT -
MSRI-UP MSRI-UP 2023: Topological Data Analysis
Organizers: Federico Ardila (San Francisco State University), LEAD Maria Mercedes Franco (Queensborough Community College (CUNY)), Rebecca Garcia (Colorado College), Jose Perea (Northeastern University), Candice Price (Smith College), Robin Wilson (Loyola Marymount University)The MSRI-UP summer program is designed to serve a diverse group of undergraduate students who would like to conduct research in the mathematical sciences.
In 2023, MSRI-UP will focus on Topological Data Analysis. The research program will be led by Dr. Jose Perea, Associate Professor in the Department of Mathematics and the Khoury College of Computer Sciences at Northeastern University.
Updated on Mar 07, 2024 12:48 PM PST -
Summer Graduate School Formalization of Mathematics (SLMath)
Organizers: Jeremy Avigad (Carnegie Mellon University), Heather Macbeth (Fordham University at Lincoln Center), Patrick Massot (Université Paris-Saclay)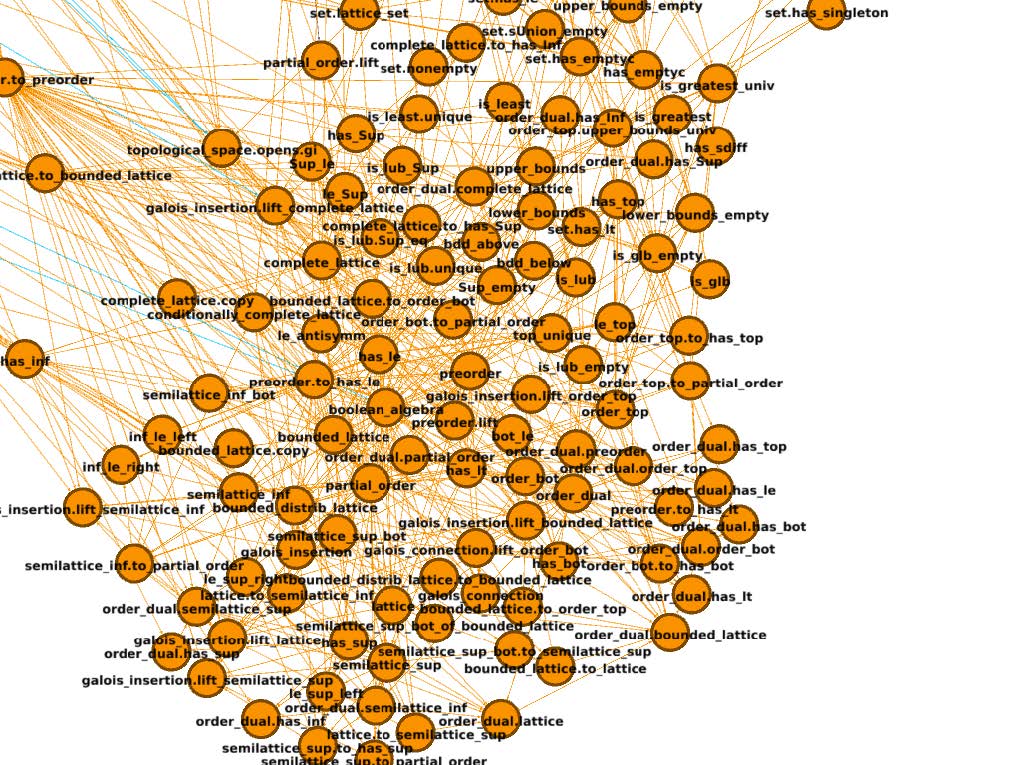 Some basic concepts in mathlib and the dependencies between them
Some basic concepts in mathlib and the dependencies between themComputational proof assistants now make it possible to develop global, digital mathematical libraries with theorems that are fully checked by computer. This summer school will introduce students to the new technology and the ideas behind it, and will encourage them to think about the goals and benefits of formalized mathematics. Students will learn to use the Lean interactive proof assistant, and by the end of the session they will be in a position to formalize mathematics on their own, join the Lean community, and contribute to its mathematical library.
Updated on Oct 20, 2023 10:07 AM PDT -
Summer Graduate School Commutative Algebra and its Interaction with Algebraic Geometry (Notre Dame)
Organizers: Steven Cutkosky (University of Missouri), LEAD Claudia Polini (University of Notre Dame), Claudiu Raicu (University of Notre Dame), Steven Sam (University of California, San Diego), Kevin Tucker (University of Illinois at Chicago)
Commutative Algebra has seen an extraordinary development in the last few years. Long standing conjectures have been proven and new connections to different areas of mathematics have been built.This summer graduate school will consist of three mini-courses (5 lectures each) on fundamental topics in commutative algebra that are not covered in the standard courses. Each course will be accompanied by problem sessions focused on research. Five general colloquium-style lectures will be given by invited scholars who will also attend the school and help with afternoon research activities.
Updated on Mar 20, 2023 01:33 PM PDT -
MAY-UP Mathematically Advancing Young Undergraduates Program (MAY-UP) [2023 Pilot Program]
Organizers: Duane Cooper (Morehouse College), Shelby Wilson (Johns Hopkins University Applied Physics Lab)2023 Pilot Program: The goal of MAY-UP is to provide students with a glimpse into Linear Algebra; and the ways in which this topic may arise both theoretically and computationally in their future studies. Material will include an introduction to matrices as well as basic matrix operations. We will also provide students with introductory programming skills in Python, including development environment setup and matrix manipulations via code.
Updated on Apr 18, 2024 06:03 AM PDT -
Workshop May 12, a Celebration for Women in Mathematics (2023)
Organizers: Ini Adinya (University of Ibadan), Masha Albrecht (Berkeley High School), Romina Arroyo (Universidad Nacional de Cordoba), Maria-Grazia Ascenzi (University of California Los Angeles), Mirela Ciperiani (University of Texas, Austin), Donatella Danielli (Arizona State University), Shanna Dobson (University of California, Riverside), Malena Espanol (Arizona State University), Olubunmi Fadipe-Joseph (University of Ilorin), Anna Fino (Università di Torino), Natalia Garcia-Fritz (Pontificia Universidad Católica de Chile), Adi Glucksam (Northwestern University), Céleste Hogan (Texas Tech University), Kuei-Nuan Lin (Pennsylvania State University), Zheng Liu (University of California, Santa Barbara), Liangbing Luo (Lehigh University), LEAD Ornella Mattei (San Francisco State University), Julia Plavnik (Indiana University), Palina Salanevich (Universiteit Utrecht), Ramdorai Sujatha (University of British Columbia)The Simons Laufer Mathematical Sciences Institute (SLMath), formerly MSRI, celebrates May 12 with a panel discussion and social event open to all on the topic "Pathways in Mathematics". This is a hybrid event taking place on Zoom and in person at SLMath and satellite institutions.
Updated on May 17, 2023 02:43 PM PDT -
Workshop MSRI / SLMath 40th Anniversary Symposium
Organizers: Hélène Barcelo (MSRI / Simons Laufer Mathematical Sciences Institute (SLMath)), Charles Fefferman (Princeton University), Dan Freed (Harvard University), Kristin Lauter (Facebook AI Research (FAIR) North America at Meta), Dusa McDuff (Barnard College), Andrei Okounkov (Columbia University; University of California, Berkeley), Tatiana Toro (MSRI / Simons Laufer Mathematical Sciences Institute (SLMath))
In 2022-23, SLMath (formerly MSRI) celebrates 40 years of serving the mathematical sciences community through our topic-focused programs and workshops, and the general public via our national and global outreach initiatives. Director Tatiana Toro and Deputy Director Hélène Barcelo invite the community to join us for a symposium to reflect upon these four decades of extraordinary activity. This celebration will feature special guest speakers, panel discussions and an evening reception.
Updated on Sep 14, 2023 05:24 PM PDT -
Workshop Critical Issues in Mathematics Education 2023: Mentoring for Equity
Organizers: Pamela Harris (University of Wisconsin-Milwaukee), Abbe Herzig (TPSE-Math), LEAD Aris Winger (Georgia Gwinnett College), Michael Young (Carnegie Mellon University)The workshop Critical Issues in Mathematics Education: Mentoring for Equity aims to reach a broad audience of faculty and students in postsecondary mathematical sciences. Participants will learn about the evidence base for effective mentoring, with a focus on culturally responsive mentoring that supports all students and faculty along their mathematical paths. The workshop includes a combination of discussion of research evidence, review and adaptation of practical tools, and explicit training in effective mentoring, including how to bring these tools back to participants’ home institutions. The workshop intertwines objectives of increasing participants’ knowledge of the scholarship on effective mentoring, and engages participants in interactive activities to develop tangible skills as mentors and as mentor-trainers. Participants should come with a growth mindset, prepared to reflect on their experiences as mentors and mentees, and actively contribute to activities that build skills for implementing best mentoring practices. This workshop will cultivate local and national mentoring communities that bring effective tools and strategies to mentoring, so that mentees can persist and thrive in research, teaching, education, and throughout their education and careers. One focus will be on addressing the individual mentoring needs of all faculty and students, including those who have been historically-marginalized in mathematics education and careers.
Updated on Mar 30, 2023 01:00 PM PDT -
Workshop Modern Math Workshop 2022
Organizers: Hélène Barcelo (MSRI / Simons Laufer Mathematical Sciences Institute (SLMath)), Philip Hammer (Institute for Mathematical and Statistical Innovation), Christian Ratsch (University of California, Los Angeles; Institute of Pure and Applied Mathematics (IPAM)), Ulrica Wilson (Morehouse College; Institute for Computational and Experimental Research in Mathematics (ICERM))ALL FUNDING FOR THIS WORKSHOP HAS BEEN ALLOCATED
As part of the Mathematical Sciences Collaborative Diversity Initiatives, the six NSF-funded U.S. mathematics institutes will host their annual SACNAS pre-conference event, the 2022 Modern Math Workshop (MMW). The Modern Math Workshop encourages undergraduates from underrepresented groups to pursue careers in the mathematical sciences, and builds research and networking opportunities among undergraduates, graduate students and recent PhDs.
Updated on Nov 29, 2022 08:49 AM PST -
Summer Graduate School Sums of Squares Method in Geometry, Combinatorics and Optimization (BIRS)
Organizers: LEAD Grigoriy Blekherman (Georgia Institute of Technology), Annie Raymond (University of Massachusetts Amherst), Cynthia Vinzant (University of Washington)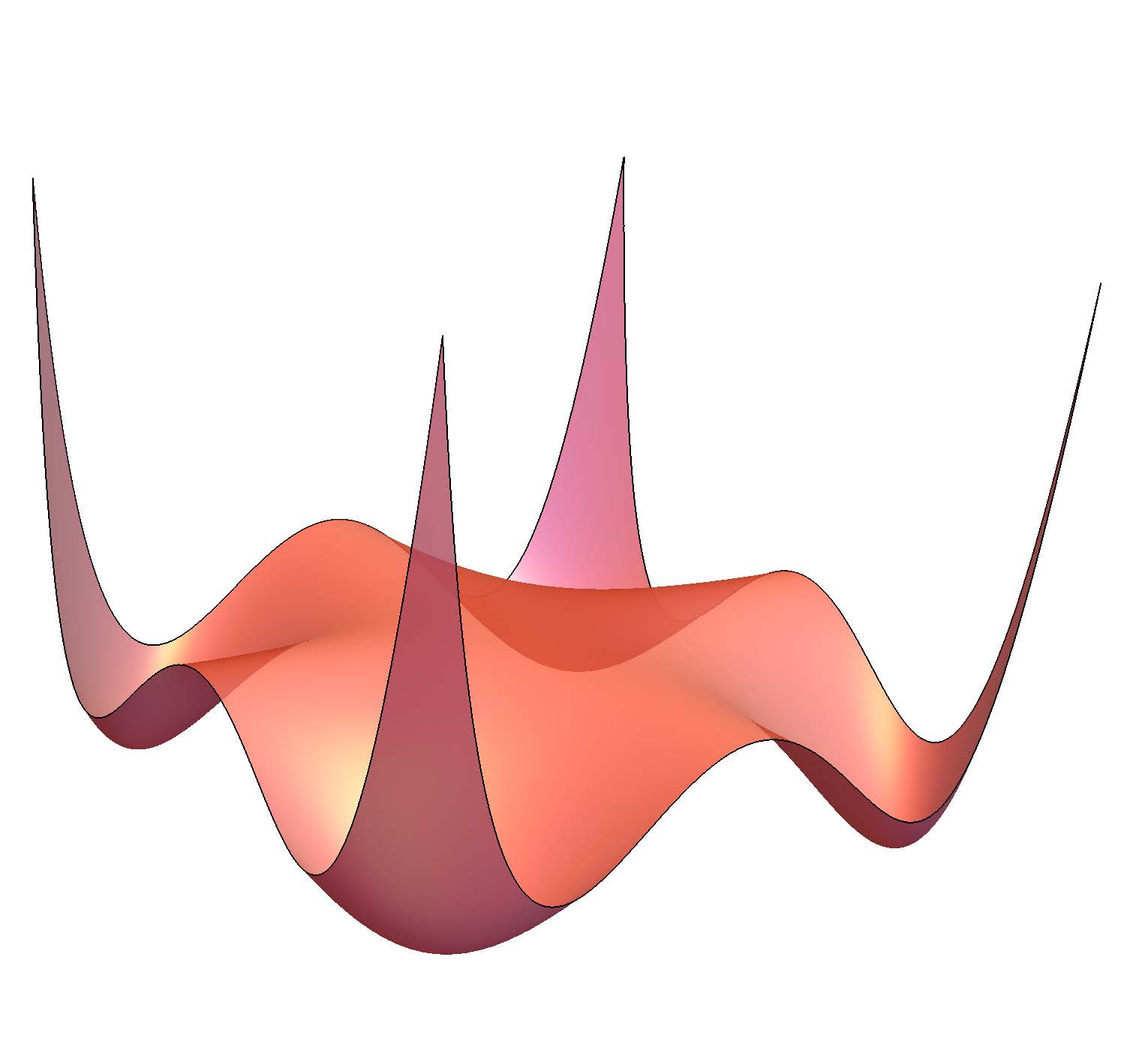 Graph of the Motzkin polynomial, which is nonnegative but not a sum of squares.
Graph of the Motzkin polynomial, which is nonnegative but not a sum of squares.The study of nonnegative polynomials and sums of squares is a classical area of real algebraic geometry dating back to Hilbert’s 17th problem. It also has rich connections to real analysis via duality and moment problems. In the last 15 years, sums of squares relaxations have found a wide array of applications from very applied areas (e.g., robotics, computer vision, and machine learning) to theoretical applications (e.g., extremal combinatorics, theoretical computer science). Also, an intimate connection between sums of squares and classical algebraic geometry has been found. Work in this area requires a blend of ideas and techniques from algebraic geometry, convex geometry and representation theory. After an introduction to nonnegative polynomials, sums of squares and semidefinite optimization, we will focus on the following three topics:
- Sums of squares on real varieties (sets defined by real polynomial equations) and connections with classical algebraic geometry.
- Sums of squares method for proving graph density inequalities in extremal combinatorics. Here addition and multiplication take place in the gluing algebra of partially labelled graphs.
- Sums of squares relaxations for convex hulls of real varieties and theta-bodies with applications in optimization.
The summer school will give a self-contained introduction aimed at beginning graduate students, and introduce participants to the latest developments. In addition to attending the lectures, students will meet in intensive problem and discussion sessions that will explore and extend the topics developed in the lectures.
Updated on Apr 07, 2022 02:41 PM PDT -
Summer Graduate School Tropical Geometry
Organizers: Renzo Cavalieri (Colorado State University), Hannah Markwig (Eberhard-Karls-Universität Tübingen), Dhruv Ranganathan (University of Cambridge)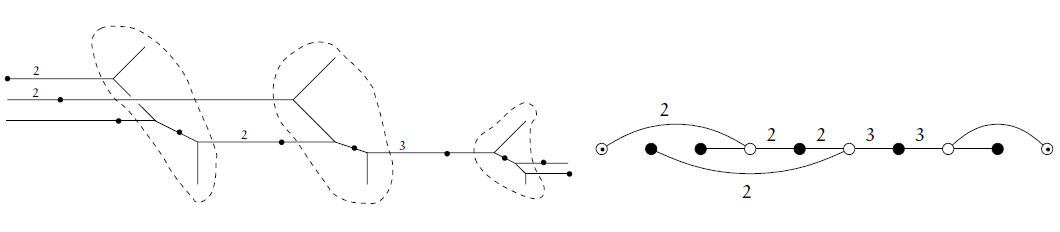 A tropical stable map and the corresponding floor diagram
A tropical stable map and the corresponding floor diagramEnumerative geometry and the theory of moduli spaces of curves are two cornerstones of modern algebraic geometry; the two subjects have had a significant influence on each other. In the last 15 years, discrete and combinatorial methods, systematized within tropical geometry, have begun to provide new avenues of access into these two subjects. The goal of this summer school is to give students crash courses in tropical and logarithmic geometry, with a particular focus on the applications in enumerative geometry and moduli theory. The school will consist of three courses of seven lectures each:
- Enumeration of tropical curves/ by Hannah Markwig
- Curve counting in tropical and algebraic geometry by Renzo Cavalieri
- Logarithmic geometry and stable map/s by Dhruv Ranganathan
Updated on Aug 12, 2022 03:03 PM PDT -
Summer Graduate School Mathematics of Machine Learning (INdAM and Courant Institute)
Organizers: Sebastien Bubeck (Microsoft Research) Popular visualization of the MNIST dataset
Popular visualization of the MNIST datasetThis school is offered in partnership with Istituto Nazionale di Alta Matematica (INdAM) and the Courant Institute of Mathematical Sciences.
Learning theory is a rich field at the intersection of statistics, probability, computer science, and optimization. Over the last decades the statistical learning approach has been successfully applied to many problems of great interest, such as bioinformatics, computer vision, speech processing, robotics, and information retrieval. These impressive successes relied crucially on the mathematical foundation of statistical learning.
Recently, deep neural networks have demonstrated stunning empirical results across many applications like vision, natural language processing, and reinforcement learning. The field is now booming with new mathematical problems, and in particular, the challenge of providing theoretical foundations for deep learning techniques is still largely open. On the other hand, learning theory already has a rich history, with many beautiful connections to various areas of mathematics (e.g., probability theory, high dimensional geometry, game theory). The purpose of the summer school is to introduce graduate students (and advanced undergraduates) to these foundational results, as well as to expose them to the new and exciting modern challenges that arise in deep learning and reinforcement learning.
Updated on Aug 12, 2022 11:42 AM PDT -
Summer Graduate School Topological Methods for the Discrete Mathematician
Organizers: Pavle Blagojevic (Freie Universität Berlin), Florian Frick (Carnegie Mellon University), Shira Zerbib (Iowa State University)
Recently, progress in the field of topological methods in discrete mathematics has been rapid and has generated a lot of activity with the resolution of major open problems, the emergence of new lines of inquiry, and the development of new tools. These exciting new developments have not been digested into a textbook treatment. The two main goals of this school are to:
- Provide graduate students with a thorough introduction to novel topological techniques and to a handful of their applications in the fields of combinatorics and discrete geometry with short glimpses into mathematical mechanics and algorithm complexity.
- Expose students to current research, and guide them in research on open problems in discrete mathematics using modern topological tools.
The summer school will lead participants from appealing, simple-to-state problems at confluence of combinatorics, geometry, and topology to sophisticated topological methods that are required for their resolution. In recent years topological methods have found numerous novel applications in mathematics and beyond, such as in data science, machine learning, economics, the social sciences, and biology. The problems we will discuss are particularly well-suited to rapidly put students in a position to approach related research questions.
Updated on Feb 14, 2023 01:39 PM PST -
Summer Graduate School MSRI-NCTS Joint Summer School: Recent Topics in Well Posedness
Organizers: Jungkai Chen (National Taiwan University), Mimi Dai (University of Illinois at Chicago), Yoshikazu Giga (University of Tokyo), Tsuyoshi Yoneda (Hitotsubashi University) Fluid-flow stream function color-coded by vorticity in 3D flat torus calculated by K. Nakai (The University of Tokyo)
Fluid-flow stream function color-coded by vorticity in 3D flat torus calculated by K. Nakai (The University of Tokyo)This school is offered in partnership with the National Center for Theoretical Sciences.
The purpose of the workshop is to introduce graduate students to fundamental results on the Navier-Stokes and the Euler equations, with special emphasis on the solvability of its initial value problem with rough initial data as well as the large time behavior of a solution. These topics have long research history. However, recent studies clarify the problems from a broad point of view, not only from analysis but also from detailed studies of orbit of the flow.
Updated on Aug 12, 2022 11:40 AM PDT -
Summer Graduate School 2022 Joint PCMI School: Number Theory Informed by Computation
Organizers: Jennifer Balakrishnan (Boston University), Rafe Mazzeo (Stanford University), Bjorn Poonen (Massachusetts Institute of Technology), Akshay Venkatesh (Institute for Advanced Study)The PCMI graduate summer school program in 2022 will consist of a sequence of 11 minicourses. The lecturers and topics for these minicourses are listed below. Each minicourse is accompanied by a problem session. The topics are arranged so that there is good material and opportunities for learning both for less experienced students as well as more advanced students. Beyond their attendance in these minicourse sessions, all graduate participants will be able to take part in the substantial other benefits of a PCMI session. This includes the opportunity to interact with the researchers in residence and take part in the research seminar component of PCMI. Many graduate students also interact in significant ways with the undergraduate cohort,,the undergraduate faculty cohort, and may also participate in the many pedagogically focused activities which form part of the K-12 Teacher Leadership Program and the Workshop for Equity in Mathematics Education. PCMI includes numerous cross-program activities to help members from all these groups interact with one another.
Updated on Feb 02, 2022 03:52 PM PST -
Summer Graduate School Metric Geometry and Geometric Analysis (Oxford, United Kingdom)
Organizers: LEAD Cornelia Drutu (University of Oxford), Panos Papazoglou (University of Oxford)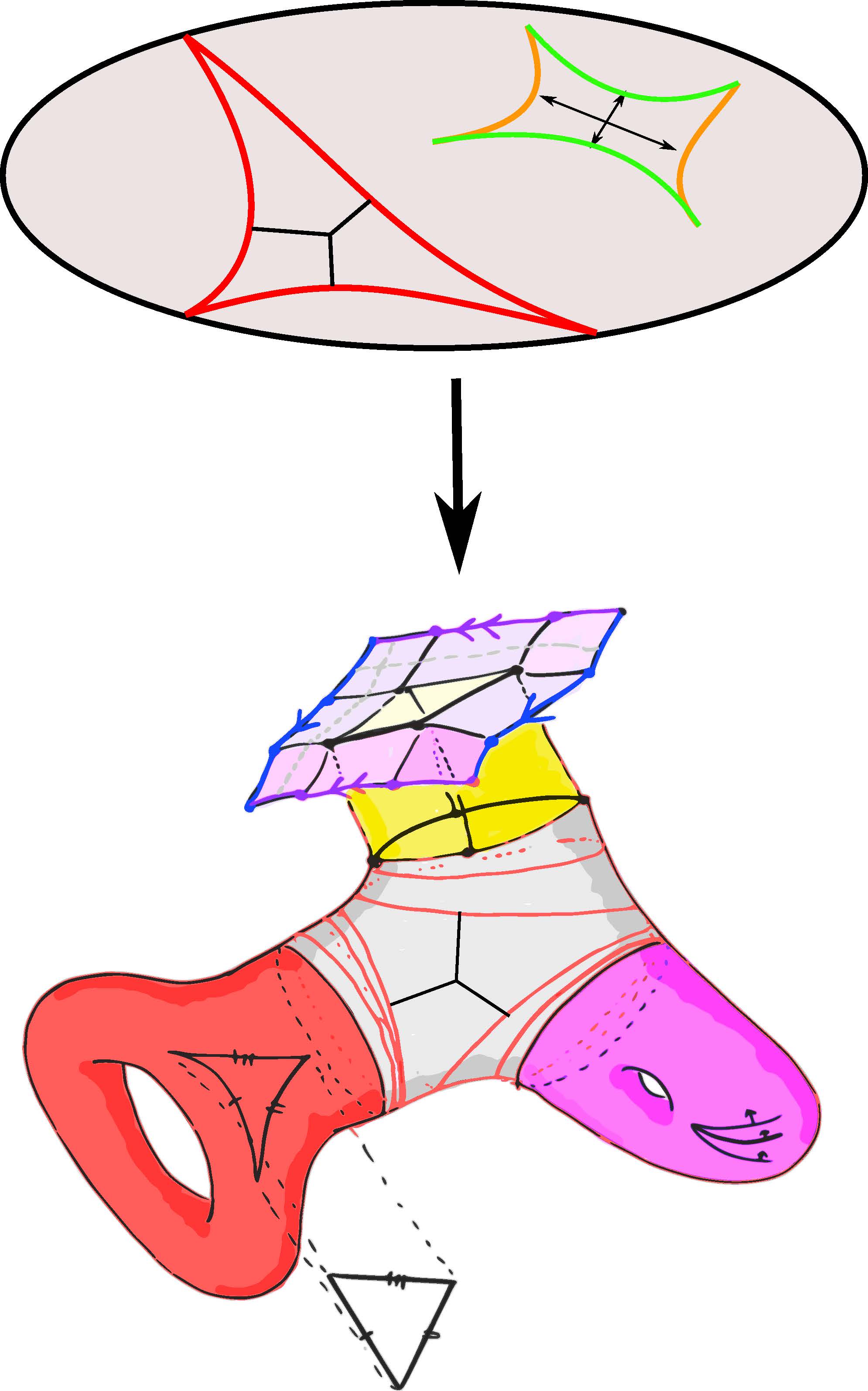 Several geometric ideas in the context of a surface: hyperbolic metric, CAT(0) inequality, Gromov hyperbolicity/coarse median geometry, nonpositively-curved square tiling, Besikovitch inequality. (Picture by M. Hagen and A. Sisto.)
Several geometric ideas in the context of a surface: hyperbolic metric, CAT(0) inequality, Gromov hyperbolicity/coarse median geometry, nonpositively-curved square tiling, Besikovitch inequality. (Picture by M. Hagen and A. Sisto.)The purpose of the summer school is to introduce graduate students to key mainstream directions in the recent development of geometry, which sprang from Riemannian Geometry in an attempt to use its methods in various contexts of non-smooth geometry. This concerns recent developments in metric generalizations of the theory of nonpositively curved spaces and discretizations of methods in geometry, geometric measure theory and global analysis. The metric geometry perspective gave rise to new results and problems in Riemannian Geometry as well.
All these themes are intertwined and have developed either together or greatly influencing one another. The summer school will introduce some of the latest developments and the remaining open problems in these very modern areas, and will emphasize their synergy.
Updated on Feb 14, 2022 12:29 PM PST