MSRI Summer Graduate Schools

The Institute's Summer Graduate Schools are intended to provide graduate students with the opportunity to learn from the top researchers in their fields, both in Berkeley and at partner institutions around the world. MSRI covers local expenses as well as partial travel expenses for accepted students.
Eligibility: Graduate students from MSRI Academic Sponsoring Institutions or from the mathematics department of any U.S. institution are eligible to be nominated by their Director of Graduate Studies. Admission is on a first-come, first-served basis up to the limits of the capacity of the school. Early nominations are not accepted.
MSRI is committed to the principles of Equal Opportunity and Affirmative Action. Women and underrepresented minorities in the mathematical sciences are encouraged to speak to their Director of Graduate Studies to request nomination.

Scientific Workshops
As part of Fall and Spring semester scientific research programs, MSRI hosts a Connections for Women Workshop and an Introductory Workshop on each program's research topic. These workshops are often appropriate for graduate students, when the topic matches their research interest. These workshops typically take place early in each semester's schedule.
To learn about upcoming workshops, join the MSRI newsletter email list, or visit our Workshops page to see scheduled events.
Program Associates
MSRI welcomes a limited number of advanced graduate students as Program Associates during periods when their thesis advisors are in residence at MSRI. Nominations are submitted by invited members in the semester prior to their residency at MSRI.
Marie A. Vitulli Graduate Fellowship
 MSRI is pleased to announce a new fellowship opportunity. Beginning in academic year 2020-21, the Marie A. Vitulli Graduate Fellowship will support one advanced graduate student in mathematics, per academic year, to attend an MSRI program with their advisor.
MSRI is pleased to announce a new fellowship opportunity. Beginning in academic year 2020-21, the Marie A. Vitulli Graduate Fellowship will support one advanced graduate student in mathematics, per academic year, to attend an MSRI program with their advisor.
Eligibility: Candidates are nominated by their advisor, who must hold a membership in one of MSRI's semester long programs. Both the advisor and the candidate must commit to being in residence at MSRI for the entire semester. Nominations will be requested from advisors in early February of each year.
The fellowship is a gift of Marie A. Vitulli, University of Oregon professor emerita and director of the university’s Women in Math Project. Dr. Vitulli is a Fellow of the Association for Women in Mathematics (Class of 2019). She was elected a Fellow of the American Mathematical Society (Class of 2020), for “contributions to commutative algebra, and for service to the mathematical community particularly in support of women in mathematics''.
Current SummerSchools
Upcoming SummerSchools
-
Séminaire de Mathématiques Supérieures 2024: Flows and Variational Methods in Riemannian and Complex Geometry: Classical and Modern Methods (Montréal, Canada)
Organizers: Vestislav Apostolov (Université du Québec à Montréal), Eleonora Di Nezza (Institut de Mathématiques de Jussieu), Pengfei Guan (McGill University), Spiro Karigiannis (University of Waterloo), Julien Keller (Université du Québec à Montréal), Alina Stancu (Concordia University), Valentino Tosatti (New York University, Courant Institute)
This school will present various developments in Riemannian and Kähler geometry around the notion of curvature seen as a tool to describe and understand the geometry of the objects. The school will give graduate students the opportunity to learn key ideas and techniques of the field, with an emphasis on solidifying foundations in view of potential future research. The first week will be centered around the question of the existence of Kähler metrics with special curvature properties and the famous Yau-Tian-Donaldson conjecture. The second week will focus on geometric flows in Riemannian and complex geometry.
Updated on Mar 18, 2024 02:15 PM PDT -
Special Geometric Structures and Analysis (St. Mary's College)
Organizers: Costante Bellettini (University College London), LEAD Eleonora Di Nezza (Institut de Mathématiques de Jussieu), Song Sun (University of California, Berkeley) a Calabi-Yau manifold
a Calabi-Yau manifoldThis summer school will serve as an introduction to the SLMath program "Special geometric structures and analysis". There will be two mini-courses: one in Geometric Measure theory and the other in Microlocal Analysis. The aim is to give the basic notions of two subjects also treated during the program.
Updated on Apr 05, 2024 09:40 PM PDT -
Particle interactive systems: Analysis and computational methods (SLMath)
Organizers: LEAD Irene M. Gamba (University of Texas, Austin), Francois Golse (École Polytechnique), Qin Li (University of Wisconsin-Madison), Chiara Saffirio (Universität Basel)
This summer school will focus on the introductory notions related to the passage of Newtonian and quantum many-body dynamics to kinetic collisional models of Boltzmann flow models arising in statistical sciences in connection to model reductions when continuum macro dynamics arises; and their numerical schemes associated to transport of kinetic processes in classical and data driven mean field dynamics incorporating recent tools from computational kinetics and data science tools. There will be two sets of lectures: “From Newton to Boltzmann to Fluid dynamics”, and “Kinetic collisional theory in mean field regimes: analysis, discrete approximations, and applications”. Each lecture series will be accompanied by a collaboration session, led by the lecturer and teaching assistants. The purpose of the collaboration sessions is to encourage and strengthen higher-level thinking of the materials taught in the lectures and to direct further reading for interested students. Interactive learning activities will be conducted. For example, students will be given problem sets associated with the lectures and will work in small groups to discuss concepts and/or find solutions to assigned problems. The students will also be encouraged to give oral or poster presentations on their solutions or other materials relevant to the course.
Updated on Apr 10, 2024 02:59 PM PDT -
Introduction to Quantum-Safe Cryptography (IBM Zurich)
Organizers: Jonathan Bootle (IBM Zürich Research Laboratory), Luca De Feo (IBM Zürich Research Laboratory)
This two week summer school, jointly organized by SLMath with IBM Zurich, will introduce students to the mathematics and algorithms used in the design and analysis of quantum-safe cryptosystems. Each week will be dedicated to two of the four families of quantum-safe schemes.
Updated on Apr 16, 2024 03:42 PM PDT -
Stochastic Quantization (SLMath)
Organizers: Massimiliano Gubinelli (University of Oxford), Martina Hofmanova (Universität Bielefeld), LEAD Hao Shen (University of Wisconsin-Madison), Lorenzo Zambotti (Sorbonne Université)
This summer school will familiarize students with the basic problems of the mathematical theory of Euclidean quantum fields. The lectures will introduce some of its prominent models and analyze them via the so called “stochastic quantization” methods, involving recently developed stochastic and PDE techniques. This is an area which is highly interdisciplinary combining ideas ranging from the theory of partial differential equations, to stochastic analysis, to mathematical physics. Our goal is to bring together students who are perhaps familiar with some but not all of these subjects and teach them how to integrate these different tools to solve cutting-edge problems of Euclidean quantum field theory.
Updated on Apr 24, 2024 03:23 PM PDT -
H-principle (Sendai, Japan)
Organizers: Emmy Murphy (Princeton University), Takashi Tsuboi (RIKEN Interdisciplinary Theoretical and Mathematical Sciences Program) The image of a large sphere isometrically embedded into a small space through a C^1 embedding. (Attributions: E. Bartzos, V. Borrelli, R. Denis, F. Lazarus, D. Rohmer, B. Thibert)
The image of a large sphere isometrically embedded into a small space through a C^1 embedding. (Attributions: E. Bartzos, V. Borrelli, R. Denis, F. Lazarus, D. Rohmer, B. Thibert)This two week summer school, jointly organized by SLMath with RIKEN, will introduce graduate students to the theory of h-principles. After building up the theory from basic smooth topology, we will focus on more recent developments of the theory, particularly applications to symplectic and contact geometry, fluid dynamics, and foliation theory.
h-principles in smooth topology (Emmy Murphy)
Riemannian geometry and applications to fluid dynamics (Dominik Inauen)
Contact and symplectic flexibility (Emmy Murphy)
Foliation theory and diffeomorphism groups (Takashi Tsuboi)Updated on Apr 17, 2024 10:55 AM PDT -
Koszul Duality in the Local Langlands Program (St. Mary's College)
Organizers: Clifton Cunningham (University of Calgary), LEAD Sarah Dijols (University of Calgary)
This summer school provides the mathematical background to recognize Koszul duality in representation theory. The school is especially oriented toward applications in the local Langlands program, with an emphasis on real groups. As Koszul duality patterns have been initially observed in the context of Hecke algebras, our school will also introduce the students to Hecke algebras and their categorifications.
Updated on Apr 12, 2024 11:27 PM PDT -
Introduction to the Theory of Algebraic Curves (UC Berkeley)
Organizers: Izzet Coskun (University of Illinois, Chicago), Eric Larson (Brown University), LEAD Hannah Larson (University of California, Berkeley), Isabel Vogt (Brown University)
In the last few years, there have been extraordinary developments in many aspects of curve theory. Beginning with many examples in low genus, this summer school will introduce the participants to the background behind these developments in the following areas:
- moduli spaces of stable curves
- Brill–Noether theory
- the extrinsic geometry of the curves in projective space
We will also include an introduction to some open problems at the forefront of these active areas.
Updated on Apr 19, 2024 10:16 AM PDT -
Mathematics of General Relativity and Fluids (FORTH, Greece)
Organizers: LEAD Mihalis Dafermos (Princeton University), Grigorios Fournodavlos (University of Crete), Juhi Jang (University of Southern California), Igor Rodnianski (Princeton University) ALCF Visualization and Data Analytics Team; Adam Burrows and the Princeton Supernova Theory Group, Princeton University
ALCF Visualization and Data Analytics Team; Adam Burrows and the Princeton Supernova Theory Group, Princeton UniversityThis summer school will give an accessible introduction to the mathematical study of general relativity, a field which in the past has had barriers to entry due to its interdisciplinary nature, and whose study has been concentrated at specific institutions, to a wider audience of students studying at institutions throughout the U.S., Europe and Greece. Another goal of the summer school will be to demonstrate the common underlying mathematical themes in many problems which traditionally have been studied by separate research communities.
Updated on Mar 19, 2024 04:24 PM PDT -
Analysis of Partial Differential Equations (Okinawa Institute of Science and Technology)
Organizers: Ugur Abdulla (Okinawa Institute of Science and Technology), Gui-Qiang Chen (University of Oxford)This two week summer school, jointly organized by SLMath with OIST, will offer the following two mini-courses:
- Measure-theoretical analysis, divergence-measure fields, and nonlinear PDEs of divergence form
This course will present some recent developments in the theory of divergence-measure fields via measure-theoretic analysis and its applications to the analysis of nonlinear PDEs of conservative form – nonlinear conservation laws. - Perron’s method and Wiener-type criteria in the potential theory of elliptic and parabolic PDEs
This course will present some recent developments precisely characterizing the regularity of the point at ∞ for second order elliptic and parabolic PDEs and broadly extending the role of the Wiener test in classical analysis.
Updated on Apr 19, 2024 12:54 PM PDT - Measure-theoretical analysis, divergence-measure fields, and nonlinear PDEs of divergence form
-
Multigraded and differential graded methods in commutative algebra (St. Mary's College)
Organizers: Michael Brown (Auburn University), Claudia Miller (Syracuse University) Product of projective lines embedded in projective 3-space
Product of projective lines embedded in projective 3-spaceThis summer graduate school focuses on modern homological techniques in commutative algebra, specifically those involving multigraded and differential graded structures. These topics have a long and rich history, but neither is generally covered in graduate courses. Moreover, recent developments have exhibited exciting interplay between the two subjects.
The purpose of the school is to introduce the participants to modern themes on these topics, including Koszul duality for toric varieties and differential graded algebra structures on resolutions. The school will consist of two lectures each day and carefully planned problem sessions designed to reinforce the foundational material, with an emphasis on using computational tools such as the symbolic algebra program Macaulay2.
Updated on Apr 16, 2024 12:43 PM PDT -
Mathematical Spin Glass Theory (Courant, NY)
Organizers: Antonio Auffinger (Northwestern University), Wei-Kuo Chen (University of Minnesota), LEAD Eliran Subag (Weizmann Institute of Science)
While their original aim was to explain the strange behavior of certain magnetic alloys, the study of spin glass models has led to a far-reaching and beautiful physical theory whose techniques have been applied to a myriad of problems in theoretical computer science, statistics, optimization and biology. As many of the physical predictions can be formulated as purely mathematical questions, often extremely hard, about large random systems in high dimensions, in recent decades a new area of research has emerged in probability theory around these problems.
Mathematically, a mean-field spin glass model is a Gaussian process (random function) on the discrete hypercube or the sphere in high dimensions. A fundamental challenge in their analysis is, roughly speaking, to understand the size and structure of their super-level sets as the dimension tends to infinity, which are often studied through smooth objects like the free energy and Gibbs measure whose origin is in statistical physics. The aim of the summer school is to introduce students to landmark results on the latter while emphasizing the techniques and ideas that were developed to obtain them, as well as exposing the students to some recent research topics.
Updated on Apr 19, 2024 03:00 PM PDT -
Statistical Optimal Transport (St. Mary's College)
Organizers: LEAD Promit Ghosal (Brandeis University), Jonathan Niles-Weed (New York University, Courant Institute), Marcel Nutz (Columbia University)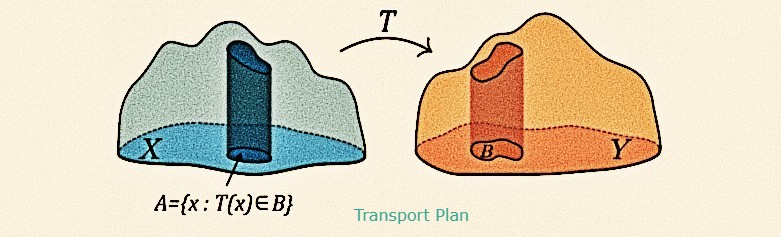
This summer school offers an exceptional opportunity for participants to delve into the intricate realm of statistical optimal transport theory. This captivating field stands at the crossroads of multiple disciplines, drawing from a rich tapestry of mathematical insights from diverse subjects, including partial differential equations, stochastic analysis, convex geometry, statistics, and machine learning, crafting a vibrant and interdisciplinary landscape. The foremost objective of this summer school is to create a dynamic learning environment that unites students from diverse backgrounds such as PDE theory, probability, or optimal transport.
Updated on Mar 20, 2024 02:04 PM PDT -
Noncommutative Algebraic Geometry
Organizers: Pieter Belmans (University of Luxembourg), Lander Hermans (Universiteit Antwerp), Wendy Lowen (Universiteit Antwerpen), Arne Mertens (Universiteit Antwerp), Michel VAN DEN BERGH (Hasselt University), Špela Špenko (Université Libre de Bruxelles)Created on Apr 03, 2024 05:26 PM PDT -
Computer Assisted Proofs in Applied Mathematics (SLMath)
Organizers: LEAD Jonathan Jaquette (New Jersey Institute of Technology), Evelyn Sander (George Mason University)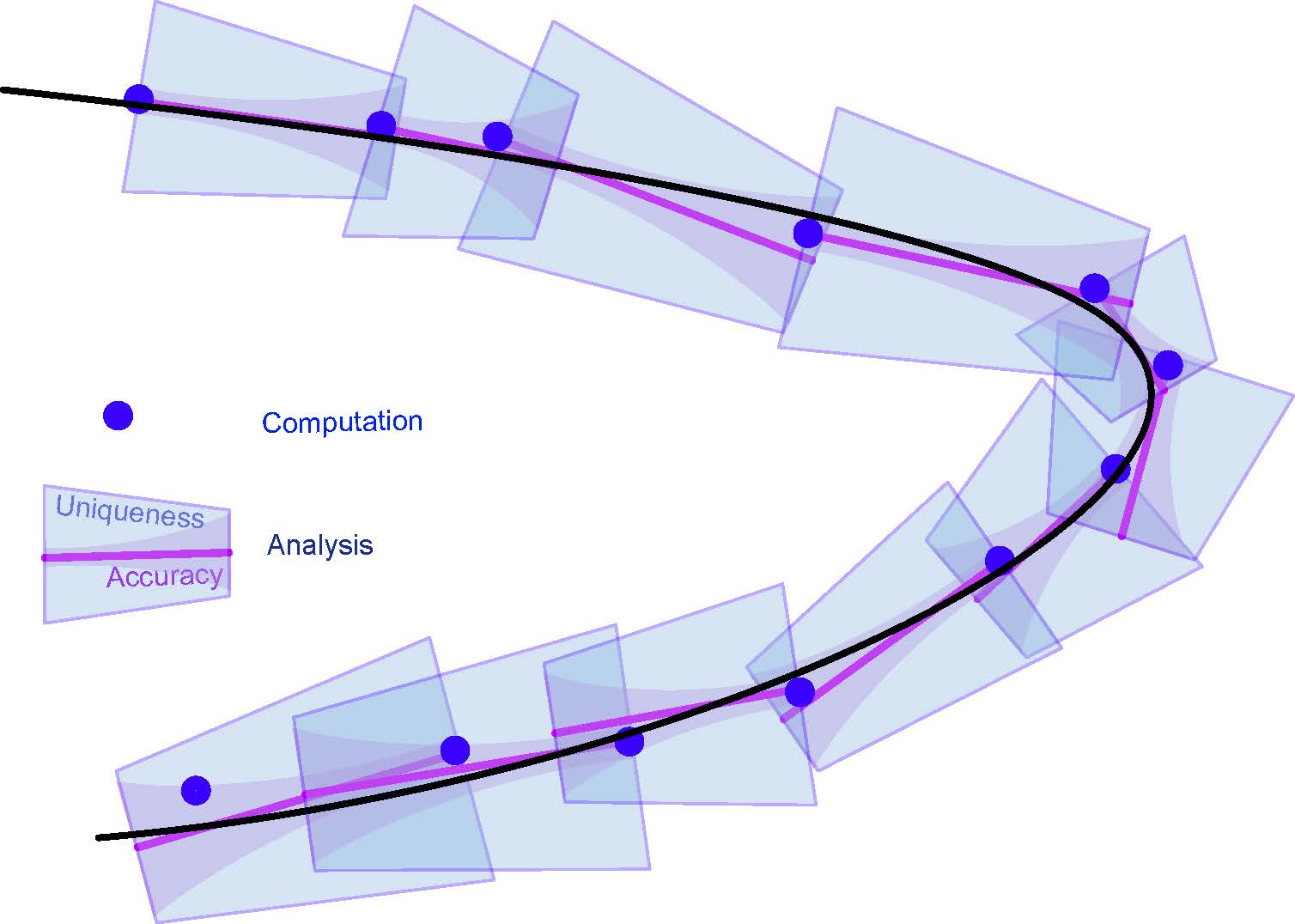
One of the core elements of applied mathematics is mathematical modeling consisting of nonlinear equations such as ODEs, and PDEs. A fundamental difficulty which arises is that most nonlinear models cannot be solved in closed form. Computer assisted proofs are at the forefront of modern mathematics and have led to many important recent mathematical advances. They provide a way of melding analytical techniques with numerical methods, in order to provide rigorous statements for mathematical models that could not be treated by either method alone. In this summer school, students will review standard computational and analytical techniques, learn to combine these techniques with more specialized methods of interval arithmetic, and apply these methods to establish rigorous results in otherwise intractable problems
Updated on Apr 08, 2024 08:55 AM PDT -
Geometry and Dynamics in Higher Rank Lie Groups (St. Mary's College)
Organizers: Richard Canary (University of Michigan), Sara Maloni (University of Virginia), Wenyu Pan (University of Toronto), Cagri Sert (University of Zurich), LEAD Tengren Zhang (National University of Singapore)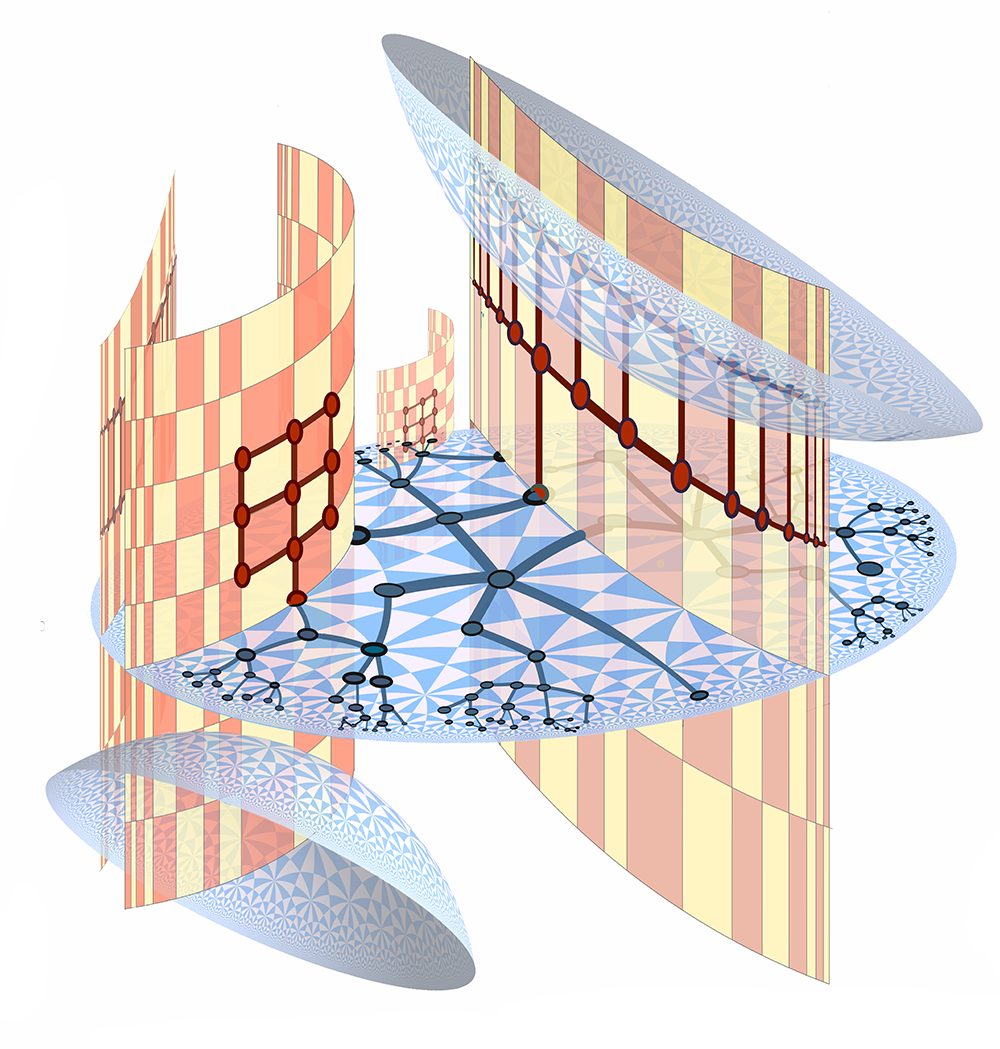 <p>Flats and hyperbolic planes in a higher rank symmetric space</p> Drawn by Steve Trettel.
<p>Flats and hyperbolic planes in a higher rank symmetric space</p> Drawn by Steve Trettel.Lie groups are central objects in modern mathematics; they arise as the automorphism groups of many homogeneous spaces, such as flag manifolds and Riemannian symmetric spaces. Often, one can construct manifolds locally modelled on these homogeneous spaces by taking quotients of their subsets by discrete subgroups of their automorphism groups. Studying such discrete subgroups of Lie groups is an active and growing area of mathematical research. The objective of this summer school is to introduce young researchers to a class of discrete subgroups of Lie groups, called Anosov subgroups.
Updated on Apr 18, 2024 08:43 AM PDT -
Topological and Geometric Structures in Low Dimensions (SLMath)
Organizers: LEAD Kenneth Bromberg (University of Utah), Kathryn Mann (Cornell University) <p>Laminations arise naturally in hyperbolic geometry and (pseudo-) Anosov flows [Image by Jeffrey Brock]</p>
<p>Laminations arise naturally in hyperbolic geometry and (pseudo-) Anosov flows [Image by Jeffrey Brock]</p>This school will serve as an introduction to the SLMath semester “Topological and Geometric Structures in Low-Dimensions”. The school consists of two mini-courses: one on Teichmüller Theory and Hyperbolic 3-Manifolds and the other on Anosov Flows on Geometric 3-Manifolds. Both topics lie at the interface of low-dimensional geometric topology (specifically, surfaces, foliations, and 3-manifolds) and low-dimensional dynamics. The first course will be targeted towards students who have completed the standard first year graduate courses in geometry, topology, and analysis while the second course will geared towards more advanced students who are closer to beginning research. However, we expect that all students will benefit from both courses.
Updated on Mar 21, 2024 09:48 AM PDT
Past SummerSchools
-
Foundations and Frontiers of Probabilistic Proofs (Zürich, Switzerland)
Organizers: Alessandro Chiesa (École Polytechnique Fédérale de Lausanne (EPFL))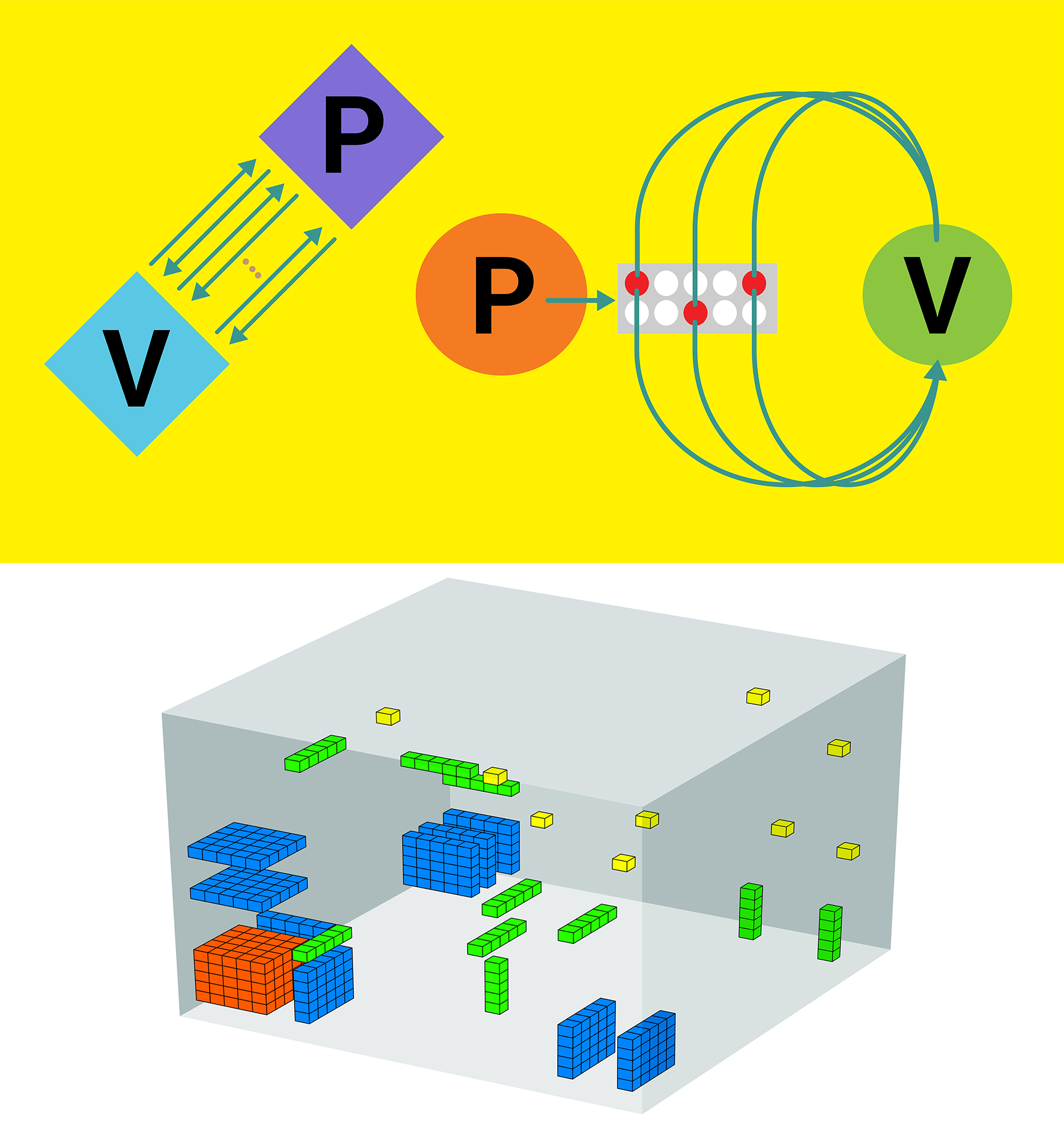 Several executions of a 3-dimensional sumcheck protocol with a random order of directions (thanks to Dev Ojha for creating the diagram)
Several executions of a 3-dimensional sumcheck protocol with a random order of directions (thanks to Dev Ojha for creating the diagram)Proofs are at the foundations of mathematics. Viewed through the lens of theoretical computer science, verifying the correctness of a mathematical proof is a fundamental computational task. Indeed, the P versus NP problem, which deals precisely with the complexity of proof verification, is one of the most important open problems in all of mathematics.
The complexity-theoretic study of proof verification has led to exciting reenvisionings of mathematical proofs. For example, probabilistically checkable proofs (PCPs) admit local-to-global structure that allows verifying a proof by reading only a minuscule portion of it. As another example, interactive proofs allow for verification via a conversation between a prover and a verifier, instead of the traditional static sequence of logical statements. The study of such proof systems has drawn upon deep mathematical tools to derive numerous applications to the theory of computation and beyond.
In recent years, such probabilistic proofs received much attention due to a new motivation, delegation of computation, which is the emphasis of this summer school. This paradigm admits ultra-fast protocols that allow one party to check the correctness of the computation performed by another, untrusted, party. These protocols have even been realized within recently-deployed technology, for example, as part of cryptographic constructions known as succinct non-interactive arguments of knowledge (SNARKs).
This summer school will provide an introduction to the field of probabilistic proofs and the beautiful mathematics behind it, as well as prepare students for conducting cutting-edge research in this area.
Updated on Oct 20, 2023 01:17 PM PDT -
Mathematics of Big Data: Sketching and (Multi-) Linear Algebra (IBM Almaden)
Organizers: Kenneth Clarkson (IBM Research Division), Lior Horesh (IBM Thomas J. Watson Research Center), Misha Kilmer (Tufts University), Tamara Kolda (MathSci.ai), Shashanka Ubaru (IBM Thomas J. Watson Research Center)
This summer school will introduce graduate students to sketching-based approaches to computational linear and multi-linear algebra. Sketching here refers to a set of techniques for compressing a matrix, to one with fewer rows, or columns, or entries, usually via various kinds of random linear maps. We will discuss matrix computations, tensor algebras, and such sketching techniques, together with their applications and analysis.
Updated on Nov 03, 2022 11:59 AM PDT -
Concentration Inequalities and Localization Techniques in High Dimensional Probability and Geometry (SLMath)
Organizers: Max Fathi (Université Paris Cité), Dan Mikulincer (Massachusetts Institute of Technology)The goal of the summer school is for the students to first become familiar with the concept of concentration of measure in different settings (Euclidean, Riemannian and discrete), and the main open problems surrounding it. The students will later become familiar with the proof techniques that involve the different types of localization and obtain expertise on the ways to apply the localization techniques. After attending the graduate school, the students are expected to have the necessary background that would give them a chance to both conduct research around open problems in concentration of measure, find new applications to existing localization techniques and perhaps also develop new localization techniques.
Updated on Oct 20, 2023 09:42 AM PDT -
Machine Learning (UC San Diego)
Organizers: Ery Arias-Castro (University of California, San Diego), Mikhail Belkin (University of California, San Diego), Yusu Wang (Univ. California, San Diego), Lily Weng (University of California, San Diego)The overarching goal of this summer school is to expose the students both to modern forms of unsupervised learning — in the form of geometrical and topological data analysis — and to supervised learning — in the form of (deep) neural networks applied to regression/classification problems. The organizers have opted for a lighter exposure to a broader range of topics. Using the metaphor of a meal, we are offering 2 + 2 samplers — geometry and topology for data analysis + theoretical and practical deep learning — rather than 1 + 1 main dishes. The main goal, thus, is to inspire the students to learn more about one or several of the topics covered in the school.
The expected learning outcomes for students attending the school are the following:
1. An introduction to how concepts and tools from geometry and topology can be leveraged to perform data analysis in situations where the data are not labeled.
2. An introduction to recent and ongoing theoretical and methodological/practical developments in the use of neural networks for data analysis (deep learning).
Updated on Aug 29, 2023 11:59 AM PDT -
Introduction to Derived Algebraic Geometry (UC Berkeley)
Organizers: Benjamin Antieau (Northwestern University), Dmytro Arinkin (University of Wisconsin-Madison)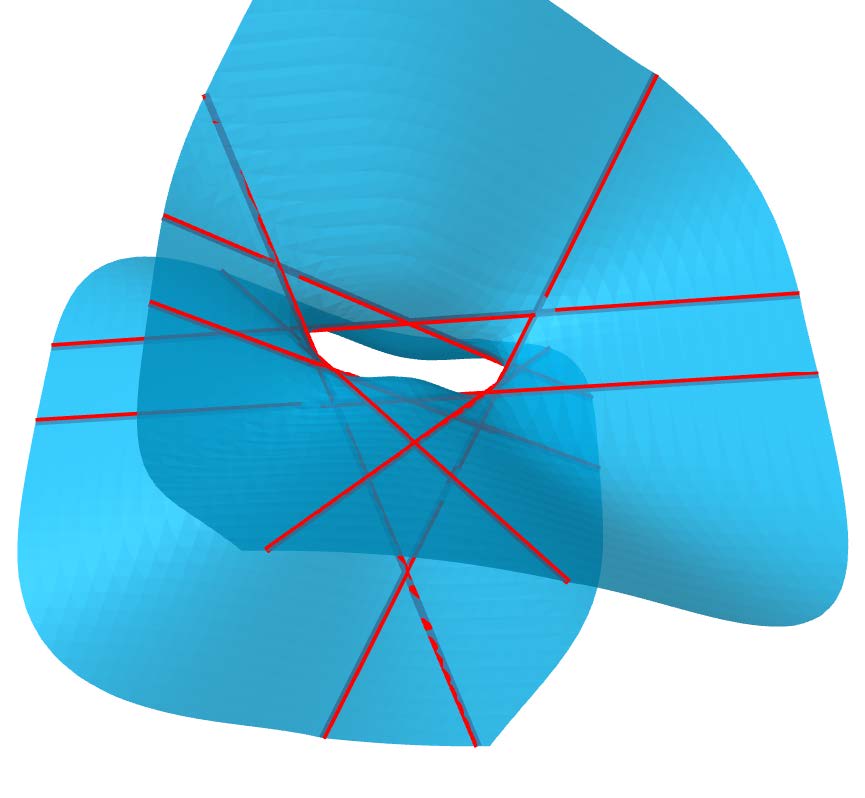 Schur quartic x 4−xy3 = z 4−zu3 and several of the 64 lines that it contains
Schur quartic x 4−xy3 = z 4−zu3 and several of the 64 lines that it containsDerived algebraic geometry is an ‘update’ of algebraic geometry using ‘derived’ (roughly speaking, homological) techniques. This requires recasting the very foundations of the field: rings have to be replaced by differential graded algebras (or other forms of derived rings), categories by higher categories, and so on. The result is a powerful set of new tools, useful both within algebraic geometry and in related areas. The school serves as an introduction to these techniques, focusing on their applications.
The school is built around two related courses on geometric (‘derived spaces’) and categorical (‘derived categories’) aspects of the theory. Our goal is to explain the key ideas and concepts, while trying to keep technicalities to a minimum.
Updated on Jun 28, 2023 04:05 PM PDT -
Topics in Geometric Flows and Minimal Surfaces (St. Mary's College)
Organizers: Ailana Fraser (University of British Columbia), Lan-Hsuan Huang (University of Connecticut), Catherine Searle (Wichita State University), Lu Wang (Yale University) Soap bubble: equilibrium solution of the rescaled mean curvature flow and constant curvature surface.
Soap bubble: equilibrium solution of the rescaled mean curvature flow and constant curvature surface.This graduate summer school will introduce students to two important and inter-related fields of differential geometry: geometric flows and minimal surfaces.
Geometric flows have had far reaching influences on numerous branches of mathematics and other scientific disciplines. An outstanding example is the completion of Hamilton’s Ricci flow program by Perelman, leading to the resolution of the Poincare conjecture and Thurston’s geometrization conjecture for 3-manifolds. In this part of the summer school, students will be guided through basic topics and ideas in the study of geometric flows.
Since Penrose used variations of volume to formulate and study black holes in general relativity (in his Nobel prize-winning work), the intriguing connections between minimal surfaces and general relativity have been a strong driving force for the modern developments of both research areas. This part of the summer school will introduce students to the basic theory of minimal submanifolds and its applications in Riemannian geometry and general relativity.
The curriculum of this program will be accessible and will have a broad appeal to graduate students from a variety of mathematical areas, introducing some of the latest developments in each area and the remaining open problems therein, while simultaneously emphasizing their synergy.
Updated on Jun 29, 2023 10:56 AM PDT -
Séminaire de Mathématiques Supérieures 2023: Periodic and Ergodic Spectral Problems (Montréal, Canada)
Organizers: Alexander Elgart (Virginia Polytechnic Institute and State University), Vojkan Jaksic (McGill University), Svetlana Jitomirskaya (University of California, Irvine), Ilya Kachkovskiy (Michigan State University), Jean Lagacé (King's College London), Leonid Parnovski (University College London)This two week school will focus on spectral theory of periodic, almost-periodic, and random operators. The main aim of this school is to teach the students who work in one of these areas, methods used in parallel problems, explain the similarities between all these areas and show them the `big picture'.
Updated on Apr 06, 2023 06:24 PM PDT -
Mathematics and Computer Science of Market and Mechanism Design (SLMath)
Organizers: Yannai Gonczarowski (Harvard University), Irene Lo (Stanford University), Ran Shorrer (Pennsylvania State University), LEAD Inbal Talgam-Cohen (Technion---Israel Institute of Technology)
This school is associated with an upcoming research program at MSRI under the same title. The goal of the school is to equip students unfamiliar with these topics with the mathematical and theoretical computer science toolbox that forms the foundation of market and mechanism design.
Updated on Jun 28, 2023 01:19 PM PDT -
Algebraic Methods for Biochemical Reaction Networks (Leipzig, Germany)
Organizers: Timo de Wolff (TU Braunschweig), LEAD Alicia Dickenstein (University of Buenos Aires), Elisenda Feliu (University of Copenhagen)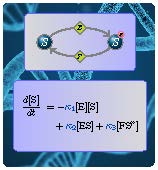 A basic enzymatic mechanism
A basic enzymatic mechanismThe aim of the course is to learn how tools from algebraic geometry (in particular, from computational and real algebraic geometry) can be used to analyze standard models in molecular biology. Particularly, these models are key ingredients in the development of Systems and Synthetic biology, two active research areas focusing on understanding, modifying, and implementing the design principles of living systems.
We will focus on the mathematical aspects of the methods, and exemplify and apply the theory to real networks, thereby introducing the participants to relevant problems and mechanisms in molecular biology. As a counterpart, however, the participants will also see how this field has in the past challenged current methods, mainly in the realm of real algebraic geometry, and has given rise to new general and purely theoretical results on polynomial equations. We will end our lectures with an overview of open questions in both fields.
Updated on Jun 15, 2023 08:39 AM PDT -
Formalization of Mathematics (SLMath)
Organizers: Jeremy Avigad (Carnegie Mellon University), Heather Macbeth (Fordham University at Lincoln Center), Patrick Massot (Université Paris-Saclay)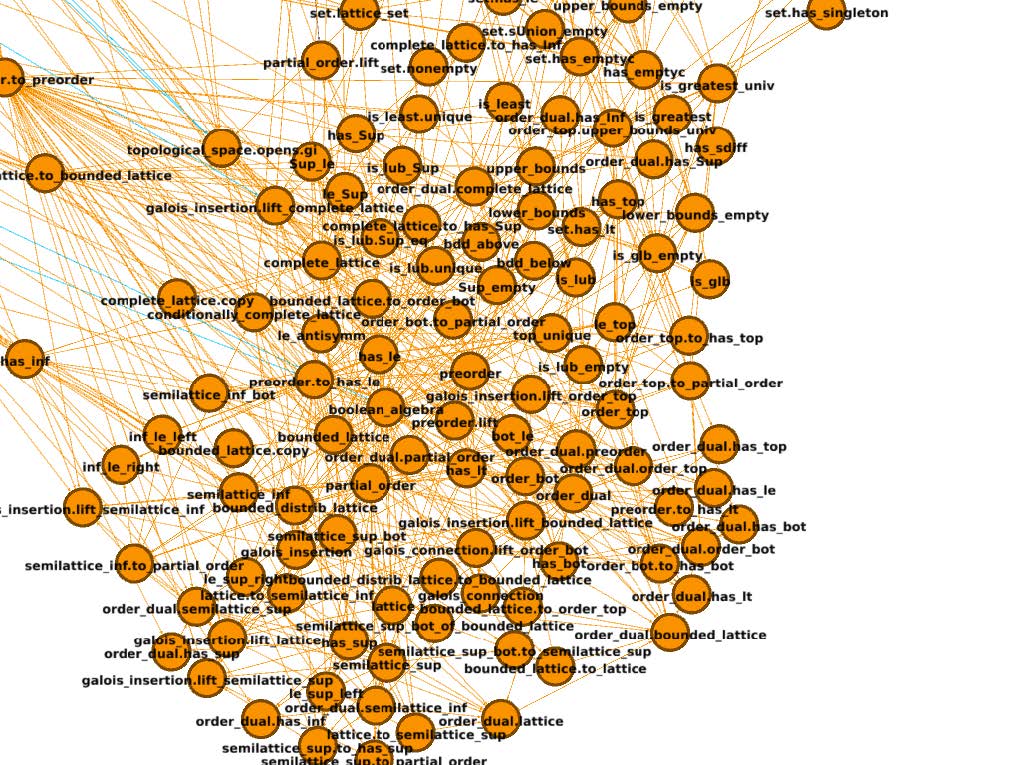 Some basic concepts in mathlib and the dependencies between them
Some basic concepts in mathlib and the dependencies between themComputational proof assistants now make it possible to develop global, digital mathematical libraries with theorems that are fully checked by computer. This summer school will introduce students to the new technology and the ideas behind it, and will encourage them to think about the goals and benefits of formalized mathematics. Students will learn to use the Lean interactive proof assistant, and by the end of the session they will be in a position to formalize mathematics on their own, join the Lean community, and contribute to its mathematical library.
Updated on Oct 20, 2023 10:07 AM PDT -
Commutative Algebra and its Interaction with Algebraic Geometry (Notre Dame)
Organizers: Steven Cutkosky (University of Missouri), LEAD Claudia Polini (University of Notre Dame), Claudiu Raicu (University of Notre Dame), Steven Sam (University of California, San Diego), Kevin Tucker (University of Illinois at Chicago)
Commutative Algebra has seen an extraordinary development in the last few years. Long standing conjectures have been proven and new connections to different areas of mathematics have been built.This summer graduate school will consist of three mini-courses (5 lectures each) on fundamental topics in commutative algebra that are not covered in the standard courses. Each course will be accompanied by problem sessions focused on research. Five general colloquium-style lectures will be given by invited scholars who will also attend the school and help with afternoon research activities.
Updated on Mar 20, 2023 01:33 PM PDT -
Sums of Squares Method in Geometry, Combinatorics and Optimization (BIRS)
Organizers: LEAD Grigoriy Blekherman (Georgia Institute of Technology), Annie Raymond (University of Massachusetts Amherst), Cynthia Vinzant (University of Washington)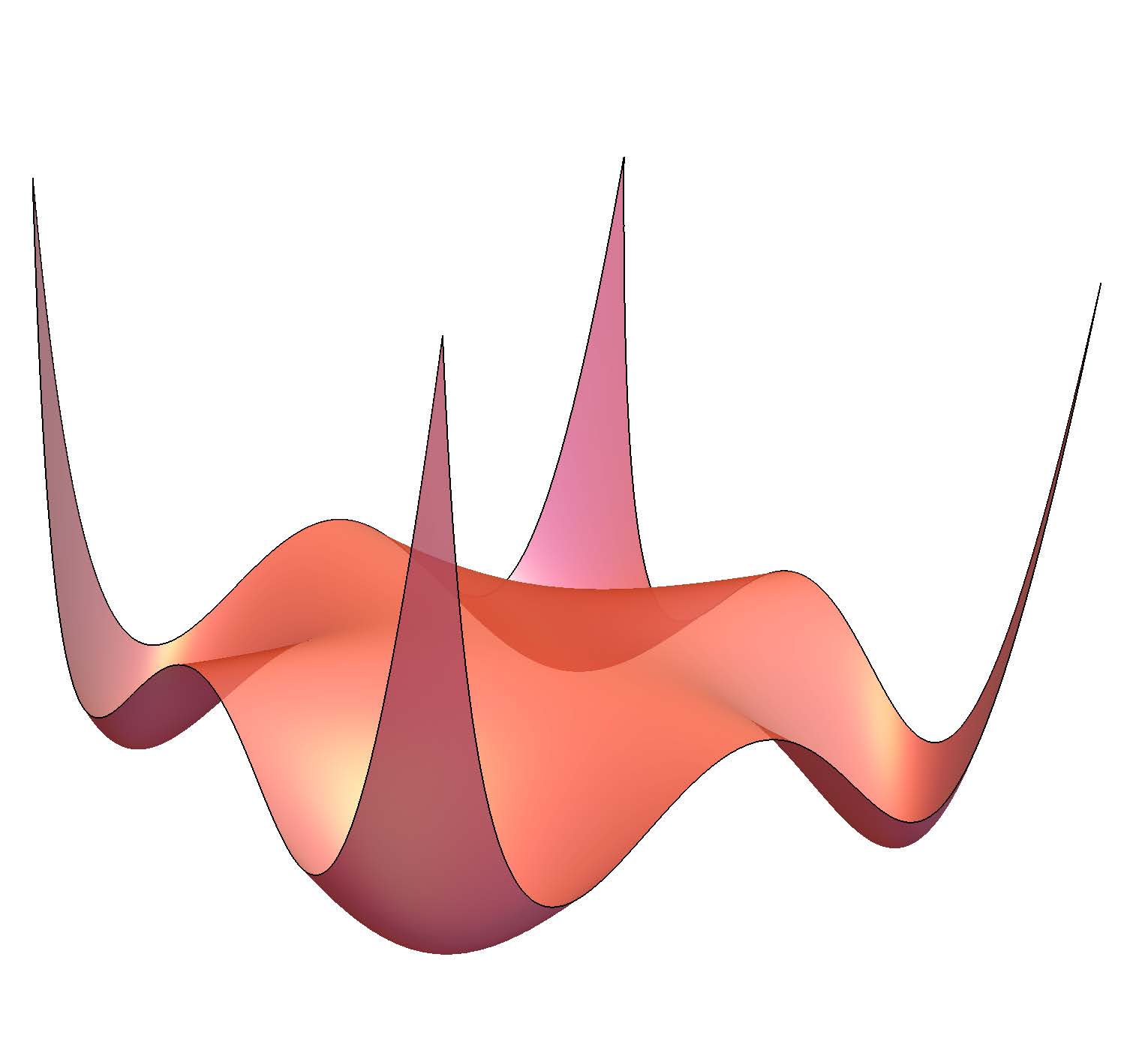 Graph of the Motzkin polynomial, which is nonnegative but not a sum of squares.
Graph of the Motzkin polynomial, which is nonnegative but not a sum of squares.The study of nonnegative polynomials and sums of squares is a classical area of real algebraic geometry dating back to Hilbert’s 17th problem. It also has rich connections to real analysis via duality and moment problems. In the last 15 years, sums of squares relaxations have found a wide array of applications from very applied areas (e.g., robotics, computer vision, and machine learning) to theoretical applications (e.g., extremal combinatorics, theoretical computer science). Also, an intimate connection between sums of squares and classical algebraic geometry has been found. Work in this area requires a blend of ideas and techniques from algebraic geometry, convex geometry and representation theory. After an introduction to nonnegative polynomials, sums of squares and semidefinite optimization, we will focus on the following three topics:
- Sums of squares on real varieties (sets defined by real polynomial equations) and connections with classical algebraic geometry.
- Sums of squares method for proving graph density inequalities in extremal combinatorics. Here addition and multiplication take place in the gluing algebra of partially labelled graphs.
- Sums of squares relaxations for convex hulls of real varieties and theta-bodies with applications in optimization.
The summer school will give a self-contained introduction aimed at beginning graduate students, and introduce participants to the latest developments. In addition to attending the lectures, students will meet in intensive problem and discussion sessions that will explore and extend the topics developed in the lectures.
Updated on Apr 07, 2022 02:41 PM PDT -
Tropical Geometry
Organizers: Renzo Cavalieri (Colorado State University), Hannah Markwig (Eberhard-Karls-Universität Tübingen), Dhruv Ranganathan (University of Cambridge)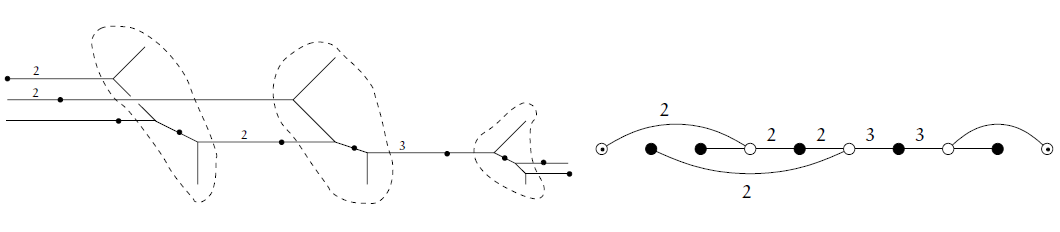 A tropical stable map and the corresponding floor diagram
A tropical stable map and the corresponding floor diagramEnumerative geometry and the theory of moduli spaces of curves are two cornerstones of modern algebraic geometry; the two subjects have had a significant influence on each other. In the last 15 years, discrete and combinatorial methods, systematized within tropical geometry, have begun to provide new avenues of access into these two subjects. The goal of this summer school is to give students crash courses in tropical and logarithmic geometry, with a particular focus on the applications in enumerative geometry and moduli theory. The school will consist of three courses of seven lectures each:
- Enumeration of tropical curves/ by Hannah Markwig
- Curve counting in tropical and algebraic geometry by Renzo Cavalieri
- Logarithmic geometry and stable map/s by Dhruv Ranganathan
Updated on Aug 12, 2022 03:03 PM PDT -
Mathematics of Machine Learning (INdAM and Courant Institute)
Organizers: Sebastien Bubeck (Microsoft Research) Popular visualization of the MNIST dataset
Popular visualization of the MNIST datasetThis school is offered in partnership with Istituto Nazionale di Alta Matematica (INdAM) and the Courant Institute of Mathematical Sciences.
Learning theory is a rich field at the intersection of statistics, probability, computer science, and optimization. Over the last decades the statistical learning approach has been successfully applied to many problems of great interest, such as bioinformatics, computer vision, speech processing, robotics, and information retrieval. These impressive successes relied crucially on the mathematical foundation of statistical learning.
Recently, deep neural networks have demonstrated stunning empirical results across many applications like vision, natural language processing, and reinforcement learning. The field is now booming with new mathematical problems, and in particular, the challenge of providing theoretical foundations for deep learning techniques is still largely open. On the other hand, learning theory already has a rich history, with many beautiful connections to various areas of mathematics (e.g., probability theory, high dimensional geometry, game theory). The purpose of the summer school is to introduce graduate students (and advanced undergraduates) to these foundational results, as well as to expose them to the new and exciting modern challenges that arise in deep learning and reinforcement learning.
Updated on Aug 12, 2022 11:42 AM PDT -
Topological Methods for the Discrete Mathematician
Organizers: Pavle Blagojevic (Freie Universität Berlin), Florian Frick (Carnegie Mellon University), Shira Zerbib (Iowa State University)
Recently, progress in the field of topological methods in discrete mathematics has been rapid and has generated a lot of activity with the resolution of major open problems, the emergence of new lines of inquiry, and the development of new tools. These exciting new developments have not been digested into a textbook treatment. The two main goals of this school are to:
- Provide graduate students with a thorough introduction to novel topological techniques and to a handful of their applications in the fields of combinatorics and discrete geometry with short glimpses into mathematical mechanics and algorithm complexity.
- Expose students to current research, and guide them in research on open problems in discrete mathematics using modern topological tools.
The summer school will lead participants from appealing, simple-to-state problems at confluence of combinatorics, geometry, and topology to sophisticated topological methods that are required for their resolution. In recent years topological methods have found numerous novel applications in mathematics and beyond, such as in data science, machine learning, economics, the social sciences, and biology. The problems we will discuss are particularly well-suited to rapidly put students in a position to approach related research questions.
Updated on Feb 14, 2023 01:39 PM PST -
MSRI-NCTS Joint Summer School: Recent Topics in Well Posedness
Organizers: Jungkai Chen (National Taiwan University), Mimi Dai (University of Illinois at Chicago), Yoshikazu Giga (University of Tokyo), Tsuyoshi Yoneda (Hitotsubashi University) Fluid-flow stream function color-coded by vorticity in 3D flat torus calculated by K. Nakai (The University of Tokyo)
Fluid-flow stream function color-coded by vorticity in 3D flat torus calculated by K. Nakai (The University of Tokyo)This school is offered in partnership with the National Center for Theoretical Sciences.
The purpose of the workshop is to introduce graduate students to fundamental results on the Navier-Stokes and the Euler equations, with special emphasis on the solvability of its initial value problem with rough initial data as well as the large time behavior of a solution. These topics have long research history. However, recent studies clarify the problems from a broad point of view, not only from analysis but also from detailed studies of orbit of the flow.
Updated on Aug 12, 2022 11:40 AM PDT -
2022 Joint PCMI School: Number Theory Informed by Computation
Organizers: Jennifer Balakrishnan (Boston University), Rafe Mazzeo (Stanford University), Bjorn Poonen (Massachusetts Institute of Technology), Akshay Venkatesh (Institute for Advanced Study)The PCMI graduate summer school program in 2022 will consist of a sequence of 11 minicourses. The lecturers and topics for these minicourses are listed below. Each minicourse is accompanied by a problem session. The topics are arranged so that there is good material and opportunities for learning both for less experienced students as well as more advanced students. Beyond their attendance in these minicourse sessions, all graduate participants will be able to take part in the substantial other benefits of a PCMI session. This includes the opportunity to interact with the researchers in residence and take part in the research seminar component of PCMI. Many graduate students also interact in significant ways with the undergraduate cohort,,the undergraduate faculty cohort, and may also participate in the many pedagogically focused activities which form part of the K-12 Teacher Leadership Program and the Workshop for Equity in Mathematics Education. PCMI includes numerous cross-program activities to help members from all these groups interact with one another.
Updated on Feb 02, 2022 03:52 PM PST -
Metric Geometry and Geometric Analysis (Oxford, United Kingdom)
Organizers: LEAD Cornelia Drutu (University of Oxford), Panos Papazoglou (University of Oxford)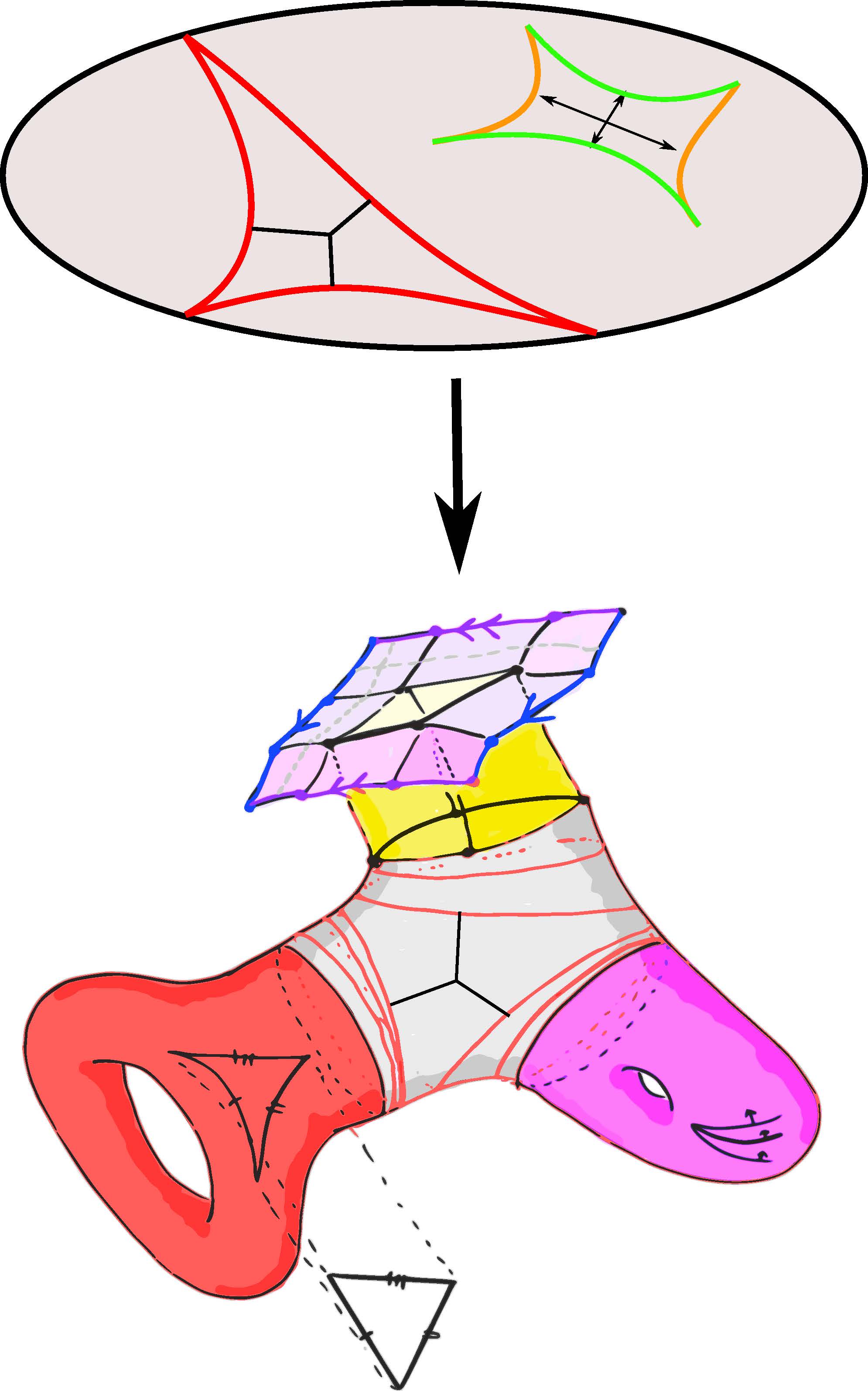 Several geometric ideas in the context of a surface: hyperbolic metric, CAT(0) inequality, Gromov hyperbolicity/coarse median geometry, nonpositively-curved square tiling, Besikovitch inequality. (Picture by M. Hagen and A. Sisto.)
Several geometric ideas in the context of a surface: hyperbolic metric, CAT(0) inequality, Gromov hyperbolicity/coarse median geometry, nonpositively-curved square tiling, Besikovitch inequality. (Picture by M. Hagen and A. Sisto.)The purpose of the summer school is to introduce graduate students to key mainstream directions in the recent development of geometry, which sprang from Riemannian Geometry in an attempt to use its methods in various contexts of non-smooth geometry. This concerns recent developments in metric generalizations of the theory of nonpositively curved spaces and discretizations of methods in geometry, geometric measure theory and global analysis. The metric geometry perspective gave rise to new results and problems in Riemannian Geometry as well.
All these themes are intertwined and have developed either together or greatly influencing one another. The summer school will introduce some of the latest developments and the remaining open problems in these very modern areas, and will emphasize their synergy.
Updated on Feb 14, 2022 12:29 PM PST -
Séminaire de Mathématiques Supérieures 2022: Floer Homotopy Theory
Organizers: Kristen Hendricks (Rutgers University), Ailsa Keating (University of Cambridge), Robert Lipshitz (University of Oregon), Liam Watson (University of British Columbia), Ben Williams (University of British Columbia) Image by Prof. Robert Lipshitz
Image by Prof. Robert LipshitzThe idea of stable homotopy refinements of Floer homology was first introduced by Cohen, Jones, and Segal in a 1994 paper, but it was only in the last decade that this idea became a key tool in low-dimensional and symplectic topology. The two crowning achievements of these techniques so far are Manolescu's use of his Pin(2)-equivariant Seiberg--Witten Floer homotopy type to resolve the Triangulation Conjecture and Abouzaid-Blumberg's use of Floer homotopy theory and Morava K-theory to prove the general Arnol'd Conjecture in finite characteristic. During this period, a range of related techniques, included under the umbrella of Floer homotopy theory, have also led to important advances, including involutive Heegaard Floer homology, Smith theory for Lagrangian intersections, homotopy coherence, and further connections between string topology and Floer theory. These in turn have sparked developments in algebraic topology, ranging from developments on Lie algebras in derived algebraic geometry to new computations of equivariant Mahowald invariants to new results on topological Hochschild homology.
The goal of the summer school is to provide participants the tools in symplectic geometry and stable homotopy theory required to work on Floer homotopy theory. Students will come away with a basic understanding of some of the key techniques, questions, and challenges in both of these fields. The summer school may be particularly valuable for participants with a solid understanding of one of the two fields who want to learn more about the other and the connections between them.Updated on May 27, 2022 09:41 AM PDT -
Random Graphs
Organizers: Louigi Addario-Berry (McGill University), Remco van der Hofstad (Technische Universiteit Eindhoven) by DeDelphin Sénizergues
by DeDelphin SénizerguesThe topic of random graphs is at the forefront of applied probability, and it is one of the central topics in multidisciplinary science where mathematical ideas are used to model and understand the real world. At the same time, random graphs pose challenging mathematical problems that have attracted the attention from probabilists and combinatorialists since the 1960, with the pioneering work of Erdös and Rényi. Around the turn of the millennium, very large data sets started to become available, and several applied disciplines started to realize that many real-world networks, even though they are from various different origins, share many fascinating features. In particular, many of such networks are small worlds, meaning that graph distances in them are typically quite small, and they are scalefree, in the sense that there are enormous differences in the number of connections that their elements make. In particular, such networks are quite different from the classical random graph models, such as proposed by Erdös and Rényi.
Updated on Jul 14, 2022 09:37 AM PDT -
Algebraic Theory of Differential and Difference Equations, Model Theory and their Applications
Organizers: LEAD Alexey Ovchinnikov (Queens College, CUNY), Anand Pillay (University of Notre Dame), Thomas Scanlon (University of California, Berkeley) Algebraic Theory Of Differential And Difference Equations, Model Theory And Their Applications
Algebraic Theory Of Differential And Difference Equations, Model Theory And Their ApplicationsThe purpose of the summer school will be to introduce graduate students to effective methods in algebraic theories of differential and difference equations with emphasis on their model-theoretic foundations and to demonstrate recent applications of these techniques to studying dynamic models arising in sciences. While these topics comprise a coherent and rich subject, they appear in graduate coursework in at best a piecemeal way, and then only as components of classes for other aims. With this Summer Graduate School, students will learn both the theoretical basis of differential and difference algebra and how to use these methods to solve practical problems. Beyond the lectures, the graduate students will meet daily in problem sessions and will participate in one-on-one mentoring sessions with the lecturers and organizers.
Updated on Jan 11, 2023 02:38 PM PST -
New Directions in Representation Theory (AMSI and U. of Hawaii, Hilo)
Organizers: Angela Coughlin (Australian Mathematical Sciences Institute), Joseph Grotowski (University of Queensland), Tim Marchant (Australian Mathematical Sciences Institute), Ole Warnaar (University of Queensland), Geordie Williamson (University of Sydney)This school is offered in partnership with the Australian Mathematical Sciences Institute and the University of Hawaii, Hilo.
Representation Theory has undergone a revolution in recent years, with the development of what is now known as higher representation theory. In particular, the notion of categorification has led to the resolution of many problems previously considered to be intractable.
The school will begin by providing students with a brief but thorough introduction to what could be termed the “bread and butter of modern representation theory”, i.e., compact Lie groups and their representation theory; character theory; structure theory of algebraic groups.
We will then continue on to a number of more specialized topics. The final mix will depend on discussions with the prospective lecturers, but we envisage such topics as:
• modular representation theory of finite groups (blocks, defect groups, Broué’s conjecture);
• perverse sheaves and the geometric Satake correspondence;
• the representation theory of real Lie groups.
Updated on Aug 12, 2022 11:38 AM PDT -
Geometric Flows (Crete, Greece)
Organizers: Nicholas Alikakos (National and Kapodistrian University of Athens (University of Athens)), Panagiota Daskalopoulos (Columbia University) photo courtesy of Panagiota Daskalopoulos
photo courtesy of Panagiota Daskalopoulos[The image on this vase from Minoan Crete, dated on 1500-2000 BC, resembles an ancient solution to the Curve shortening flow - one of the most basic geometric flows. The vase is at Heraklion Archaeological Museum]
This summer graduate school is a collaboration between MSRI and the FORTH-IACM Institute in Crete. The purpose of the school is to introduce graduate students to some of the most important geometric evolution equations. Information about the location of the summer school can be found here.
This is an area of geometric analysis that lies at the interface of differential geometry and partial differential equations. The lectures will begin with an introduction to nonlinear diffusion equations and continue with classical results on the Ricci Flow, the Mean curvature flow and other fully non-linear extrinsic flows such as the Gauss curvature flow. The lectures will also include geometric applications such as isoperimetric inequalities, topological applications such as the Poincaré onjecture, as well as recent important developments related to the study of singularities and ancient solutions.
Updated on Sep 30, 2022 12:18 PM PDT -
Integral Equations and Applications
Organizers: Fioralba Cakoni (Rutgers University), Dorina Mitrea (Baylor University), Irina Mitrea (Temple University), Shari Moskow (Drexel University) L 2 Spectra of K for apertures π 15 , · · · 14π 15 , π
L 2 Spectra of K for apertures π 15 , · · · 14π 15 , πThe field of Integral Equations has a long and distinguished history, being the driving force behind many fundamental developments in various areas of mathematics including Harmonic Analysis, Partial Differential Equations, Potential Theory, Scattering Theory, Functional Analysis, Complex Analysis, Operator Theory, Mathematical Physics and Numerical Analysis.
This school will:
- introduce graduate students to the systematic study of integral equations;
- present some of the latest theoretical advancements in the field and open problems; and
- involve participants in a hands-on discovery lab focused on deriving results about integral operators in two dimensions relevant for both the theoretical and numerical treatment of Integral Equations in two dimensions. The curriculum of this program will be accessible and will have a broad appeal to graduate students from a variety of mathematical areas (both theoretical and applied).
Updated on Aug 11, 2022 09:23 AM PDT -
Foundations and Frontiers of Probabilistic Proofs (Virtual School)
Organizers: Alessandro Chiesa (École Polytechnique Fédérale de Lausanne (EPFL)), Tom Gur (University of Warwick) Several executions of a 3-dimensional sumcheck protocol with a random order of directions (thanks to Dev Ojha for creating the diagram)
Several executions of a 3-dimensional sumcheck protocol with a random order of directions (thanks to Dev Ojha for creating the diagram)Proofs are at the foundations of mathematics. Viewed through the lens of theoretical computer science, verifying the correctness of a mathematical proof is a fundamental computational task. Indeed, the P versus NP problem, which deals precisely with the complexity of proof verification, is one of the most important open problems in all of mathematics.
The complexity-theoretic study of proof verification has led to exciting reenvisionings of mathematical proofs. For example, probabilistically checkable proofs (PCPs) admit local-to-global structure that allows verifying a proof by reading only a minuscule portion of it. As another example, interactive proofs allow for verification via a conversation between a prover and a verifier, instead of the traditional static sequence of logical statements. The study of such proof systems has drawn upon deep mathematical tools to derive numerous applications to the theory of computation and beyond.
In recent years, such probabilistic proofs received much attention due to a new motivation, delegation of computation, which is the emphasis of this summer school. This paradigm admits ultra-fast protocols that allow one party to check the correctness of the computation performed by another, untrusted, party. These protocols have even been realized within recently-deployed technology, for example, as part of cryptographic constructions known as succinct non-interactive arguments of knowledge (SNARKs).
This summer school will provide an introduction to the field of probabilistic proofs and the beautiful mathematics behind it, as well as prepare students for conducting cutting-edge research in this area.
Updated on Oct 20, 2023 01:21 PM PDT -
Random Conformal Geometry (Virtual School)
Organizers: Mario Bonk (University of California, Los Angeles), Steffen Rohde (University of Washington), LEAD Fredrik Viklund (Royal Institute of Technology) a random quasiconformal map obtained from Beltrami equation by randomly assigning the values of +-1/2 for the Beltrami coefficient on small squares subdividing the unit square
a random quasiconformal map obtained from Beltrami equation by randomly assigning the values of +-1/2 for the Beltrami coefficient on small squares subdividing the unit squareThis Summer Graduate School will cover basic tools that are instrumental in Random Conformal Geometry (the investigation of analytic and geometric objects that arise from natural probabilistic constructions, often motivated by models in mathematical physics) and are at the foundation of the subsequent semester-long program "The Analysis and Geometry of Random Spaces". Specific topics are Conformal Field Theory, Brownian Loops and related processes, Quasiconformal Maps, as well as Loewner Energy and Teichmüller Theory.
Updated on Mar 19, 2021 03:03 PM PDT -
Gauge Theory in Geometry and Topology (Virtual School)
Organizers: Lynn Heller (Universität Hannover), Francesco Lin (Columbia University), LEAD Laura Starkston (University of California, Davis), Boyu Zhang (University of Maryland) Image by Nick Schmitt
Image by Nick SchmittFigure 1. A rotationally symmetric solution to the self-duality equations on an open and dense subset of the torus. Singularities appear where the surface intersects the ideal boundary at infinity of the hyperbolic 3-space visualized by the wireframe.
Gauge theory is a geometric language used to formulate many fundamental physical phenomena, which has also had profound impact on our understanding of topology. The main idea is to study the space of solutions to partial differential equations admitting a very large group of local symmetries. Starting in the late 1970s, mathematicians began to unravel surprising connections between gauge theory and many aspects of geometric analysis, algebraic geometry and low-dimensional topology. This influence of gauge theory in geometry and topology is pervasive nowadays, and new developments continue to emerge.
The goal of the summer school is to introduce students to the foundational aspects of gauge theory, and explore their relations to geometric analysis and low-dimensional topology. By the end of the two-week program, the students will understand the relevant analytic and geometric aspects of several partial differential equations of current interest (including the Yang-Mills ASD equations, the Seiberg-Witten equations, and the Hitchin equations) and some of their most impactful applications to problems in geometry and topology.
Updated on Jun 28, 2021 12:06 PM PDT -
Mathematics of Big Data: Sketching and (Multi-) Linear Algebra (Virtual School)
Organizers: LEAD Kenneth Clarkson (IBM Research Division), Lior Horesh (IBM Thomas J. Watson Research Center), Misha Kilmer (Tufts University), Tamara Kolda (MathSci.ai), Shashanka Ubaru (IBM Thomas J. Watson Research Center)
This summer school will introduce graduate students to sketching-based approaches to computational linear and multi-linear algebra. Sketching here refers to a set of techniques for compressing a matrix, to one with fewer rows, or columns, or entries, usually via various kinds of random linear maps. We will discuss matrix computations, tensor algebras, and such sketching techniques, together with their applications and analysis.
Updated on Mar 15, 2021 03:16 PM PDT -
Sparsity of Algebraic Points (Virtual School)
Organizers: Philipp Habegger (University of Basel), LEAD Hector Pasten (Pontificia Universidad Católica de Chile) The Corvaja-Zannier proof of Siegel's theorem using subspaces. Illustrated by Sofía Pastén Vásquez.
The Corvaja-Zannier proof of Siegel's theorem using subspaces. Illustrated by Sofía Pastén Vásquez.The theory of Diophantine equations is understood today as the study of algebraic points in algebraic varieties, and it is often the case that algebraic points of arithmetic relevance are expected to be sparse.
This summer school will introduce the participants to two of the main techniques in the subject: (i) the filtration method to prove algebraic degeneracy of integral points by means of the subspace theorem, leading to special cases of conjectures by Bombieri, Lang, and Vojta, and (ii) unlikely intersections through o-minimality and bi-algebraic geometry, leading to results in the context of the Manin-Mumford conjecture, the André-Oort conjecture, and generalizations. This SGS should provide an entry point to a very active research area in modern number theory.
Updated on Mar 05, 2021 11:34 AM PST -
2021 CRM-PIMS Summer School in Probability (Virtual School)
Organizers: LEAD Louigi Addario-Berry (McGill University), Omer Angel (University of British Columbia), Alexander Fribergh (University of Montreal), Mathav Murugan (University of British Columbia), Edwin Perkins (University of British Columbia) The Sherrington-Kirkpatrick model, aka the randomly-weighted complete graph. Edge weights are indicated using grayscale. Six distinguished vertices have been randomly chosen; edges between those vertices are shaded black to form a "hidden signal".
The Sherrington-Kirkpatrick model, aka the randomly-weighted complete graph. Edge weights are indicated using grayscale. Six distinguished vertices have been randomly chosen; edges between those vertices are shaded black to form a "hidden signal".The courses in this summer school focus on mathematical models of group dynamics, how to describe their dynamics and their scaling limits, and the connection to discrete and continuous optimization problems.
The phrase "group dynamics" is used loosely here -- it may refer to species migration, the spread of a virus, or the propagation of electrons through an inhomogeneous medium, to name a few examples. Very commonly, such systems can be described via stochastic processes which approximately behave like the solution of an appropriate partial differential equation in the large-population limit.
Updated on Aug 09, 2021 02:04 PM PDT -
Séminaire de Mathématiques Supérieures 2021: Microlocal Analysis: Theory and Applications (Virtual School)
Organizers: Suresh Eswarathasan (Dalhousie University), Dmitry Jakobson (McGill University), Katya Krupchyk (University of California, Irvine), Stephane Nonnenmacher (Université de Paris XI)Microlocal analysis originated in the study of linear partial differential equations (PDEs) in the high-frequency regime, through a combination of ideas from Fourier analysis and classical Hamiltonian mechanics. In parallel, similar ideas and methods had been developed since the early times of quantum mechanics, the smallness of Planck’s constant allowing to use semiclassical methods. The junction between these two points of view (microlocal and semiclassical) only emerged in 1970s, and has taken its full place in the PDE community in the last 20 years. This methodology resulted in major advances in the understanding of linear and nonlinear PDEs in the last 50 years. Moreover, microlocal methods continue to find new applications in diverse areas of mathematical analysis, such as the spectral theory of nonselfadjoint operators, scattering theory, and inverse problems.
Updated on Oct 20, 2023 03:17 PM PDT -
Introduction to water waves [Virtual Summer Graduate School]
Organizers: Mihaela Ifrim (University of Wisconsin-Madison), Daniel Tataru (University of California, Berkeley)Overturning wave, artistic drawing by E. IfrimDue to the COVID-19 pandemic, this summer school will be held online.
The purpose of this two weeks school is to introduce graduate students to the state of the art methods and results in the study of incompressible Euler’s equations in general, and water waves in particular. This is a research area which is highly relevant to many real life problems, and in which substantial progress has been made in the last decade.
The goal is to present the main current research directions in water waves. We will begin with the physical derivation of the equations, and present some of the analytic tools needed in study. The final goal will be two-fold, namely (i) to understand the local solvability of the Cauchy problem for water waves, as well as (ii) to describe the long time behavior of solutions.
Through the lectures and associated problem sessions, students will learn about a number of new analysis tools which are not routinely taught in a graduate school curriculum. The goal is to help students acquire the knowledge needed in order to start research in water waves and Euler equations.
Updated on Oct 20, 2023 03:25 PM PDT -
Séminaire de Mathématiques Supérieures 2020: Discrete Probability, Physics and Algorithms (Montréal, Canada) [Virtual Summer Graduate School]
Organizers: Gérard Ben Arous (New York University, Courant Institute), LEAD Alexander Fribergh (University of Montreal), Lea Popovic (Concordia University)
Due to the COVID-19 pandemic, this summer school will be held online.
Probability theory, statistics as well as mathematical physics have increasingly been used in computer science. The goal of this school is to provide a unique opportunity for graduate students and young researchers to developed multi-disciplinary skills in a rapidly evolving area of mathematics.
The topics would include spin glasses, constraint satisfiability, randomized algorithms, Monte-Carlo Markov chains and high-dimensional statistics, sparse and random graphs, computational complexity, estimation and approximation algorithms. Those topics will fall into two main categories, on the one hand problems related to spin glasses and on the other hand random algorithms.
The part of the summer school dedicated to spin glasses will be split into three parts: an introductory course about traditional spin glasses followed by two more advanced courses where spin glasses meet computer science in addition to a talk on dynamics of spin glasses. The part of the summer school on random algorithms will consist of an introductory course on phase transitions in large random structures, followed by advanced courses on theoretical bounds for computational complexity in reconstruction and inference, and on understanding rare events in random graphs and models of statistical mechanics.
The two introductory courses on spin glasses and on random algorithms will be accompanied by three exercises sessions of one hour. A one hour exercises session will follow each of the three sessions of a course for both the introductory course on spin glasses and the introductory course on random algorithms. Exercises sessions will be led by an assistant, but will primarily focus on participation of the students.
Updated on May 26, 2020 12:21 PM PDT -
Toric Varieties (National Center for Theoretical Sciences, Taipei, Taiwan)
Organizers: David Cox (Amherst College), Henry Schenck (Auburn University) This simplicial fan in 3-dimensional space
This simplicial fan in 3-dimensional spaceToric varieties are algebraic varieties defined by combinatorial data, and there is a wonderful interplay between algebra, combinatorics and geometry involved in their study. Many of the key concepts of abstract algebraic geometry (for example, constructing a variety by gluing affine pieces) have very concrete interpretations in the toric case, making toric varieties an ideal tool for introducing students to abstruse concepts.
Updated on Jul 14, 2020 04:08 PM PDT -
Mathematics of Machine Learning
Organizers: Sebastien Bubeck (Microsoft Research), Anna Karlin (University of Washington), Adith Swaminathan (Microsoft Research) Popular visualization of the MNIST dataset
Popular visualization of the MNIST datasetLearning theory is a rich field at the intersection of statistics, probability, computer science, and optimization. Over the last decades the statistical learning approach has been successfully applied to many problems of great interest, such as bioinformatics, computer vision, speech processing, robotics, and information retrieval. These impressive successes relied crucially on the mathematical foundation of statistical learning.
Recently, deep neural networks have demonstrated stunning empirical results across many applications like vision, natural language processing, and reinforcement learning. The field is now booming with new mathematical problems, and in particular, the challenge of providing theoretical foundations for deep learning techniques is still largely open. On the other hand, learning theory already has a rich history, with many beautiful connections to various areas of mathematics (e.g., probability theory, high dimensional geometry, game theory). The purpose of the summer school is to introduce graduate students (and advanced undergraduates) to these foundational results, as well as to expose them to the new and exciting modern challenges that arise in deep learning and reinforcement learning.
Updated on Aug 01, 2019 10:00 AM PDT -
H-Principle (INdAM, Cortona, Italy)
Organizers: LEAD Emmy Murphy (Princeton University), Takashi Tsuboi (RIKEN Interdisciplinary Theoretical and Mathematical Sciences Program) The image of a large sphere isometrically embedded into a small space through a C^1 embedding. (Attributions: E. Bartzos, V. Borrelli, R. Denis, F. Lazarus, D. Rohmer, B. Thibert)
The image of a large sphere isometrically embedded into a small space through a C^1 embedding. (Attributions: E. Bartzos, V. Borrelli, R. Denis, F. Lazarus, D. Rohmer, B. Thibert)This two week summer school will introduce graduate students to the theory of h-principles. After building up the theory from basic smooth topology, we will focus on more recent developments of the theory, particularly applications to symplectic and contact geometry, fluid dynamics, and foliation theory.
Updated on Aug 08, 2019 09:31 AM PDT -
Recent topics on well-posedness and stability of incompressible fluid and related topics
Organizers: LEAD Yoshikazu Giga (University of Tokyo), Maria Schonbek (University of California, Santa Cruz), Tsuyoshi Yoneda (Hitotsubashi University) Fluid-flow stream function color-coded by vorticity in 3D flat torus calculated by K. Nakai (The University of Tokyo)
Fluid-flow stream function color-coded by vorticity in 3D flat torus calculated by K. Nakai (The University of Tokyo)The purpose of the workshop is to introduce graduate students to fundamental results on the Navier-Stokes and the Euler equations, with special emphasis on the solvability of its initial value problem with rough initial data as well as the large time behavior of a solution. These topics have long research history. However, recent studies clarify the problems from a broad point of view, not only from analysis but also from detailed studies of orbit of the flow.
Updated on Aug 19, 2019 04:17 PM PDT -
Polynomial Method
Organizers: Adam Sheffer (Bernard M. Baruch College, CUNY), LEAD Joshua Zahl (University of British Columbia) from distinct distances in the plane to line incidences in R^3
from distinct distances in the plane to line incidences in R^3In the past eight years, a number of longstanding open problems in combinatorics were resolved using a new set of algebraic techniques. In this summer school, we will discuss these new techniques as well as some exciting recent developments.
Updated on Oct 20, 2023 04:16 PM PDT -
Séminaire de Mathématiques Supérieures 2019: Current trends in Symplectic Topology
Organizers: Octav Cornea (Université de Montréal), Yakov Eliashberg (Stanford University), Michael Hutchings (University of California, Berkeley), Egor Shelukhin (Université de Montréal) A Holomorphic Curve
A Holomorphic CurveSymplectic topology is a fast developing branch of geometry that has seen phenomenal growth in the last twenty years. This two weeks long summer school, organized in the setting of the Séminaire de Mathématiques Supérieures, intends to survey some of the key directions of development in the subject today thus covering: advances in homological mirror symmetry; applications to hamiltonian dynamics; persistent homology phenomena; implications of flexibility and the dichotomy flexibility/rigidity; legendrian contact homology; embedded contact homology and four-dimensional holomorphic techniques and others. With the collaboration of many of the top researchers in the field today, the school intends to serve as an introduction and guideline to students and young researchers who are interested in accessing this diverse subject.
Updated on Dec 10, 2018 04:21 PM PST -
Geometric Group Theory
Organizers: LEAD Rita Jiménez Rolland (Instituto de Matematicás, UNAM-Oaxaca), LEAD Pierre Py (Universidad Nacional Autónoma de México) Rips's δ-thin triangle condition for Gromov hyperbolicity of metric spaces (Stomatapoll)
Rips's δ-thin triangle condition for Gromov hyperbolicity of metric spaces (Stomatapoll)Geometric group theory studies discrete groups by understanding the connections between algebraic properties of these groups and topological and geometric properties of the spaces on which they act. The aim of this summer school is to introduce graduate students to specific central topics and recent developments in geometric group theory. The school will also include students presentations to give the participants an opportunity to practice their speaking skills in mathematics. Finally, we hope that this meeting will help connect Latin American students with their American and Canadian counterparts in an environment that encourages discussion and collaboration.
Updated on Jul 03, 2019 11:35 AM PDT -
Representation stability
Organizers: Thomas Church (Stanford University), LEAD Andrew Snowden (University of Michigan), Jenny Wilson (University of Michigan) An illustration of an adaptation of Quillen's classical homological stability spectral sequence argument
An illustration of an adaptation of Quillen's classical homological stability spectral sequence argumentThis summer school will give an introduction to representation stability, the study of algebraic structural properties and stability phenomena exhibited by sequences of representations of finite or classical groups -- including sequences arising in connection to hyperplane arrangements, configuration spaces, mapping class groups, arithmetic groups, classical representation theory, Deligne categories, and twisted commutative algebras. Representation stability incorporates tools from commutative algebra, category theory, representation theory, algebraic combinatorics, algebraic geometry, and algebraic topology. This workshop will assume minimal prerequisites, and students in varied disciplines are encouraged to apply.
Updated on Jul 03, 2019 03:47 PM PDT -
Random and arithmetic structures in topology
Organizers: LEAD Alexander Furman (University of Illinois at Chicago), Tsachik Gelander (Weizmann Institute of Science) The study of locally symmetric manifolds, such as closed hyperbolic manifolds, involves geometry of the corresponding symmetric space, topology of towers of its finite covers, and number-theoretic aspects that are relevant to possible constructions.The workshop will provide an introduction to these and closely related topics such as lattices, invariant random subgroups, and homological methods.Updated on Oct 20, 2023 04:22 PM PDT
The study of locally symmetric manifolds, such as closed hyperbolic manifolds, involves geometry of the corresponding symmetric space, topology of towers of its finite covers, and number-theoretic aspects that are relevant to possible constructions.The workshop will provide an introduction to these and closely related topics such as lattices, invariant random subgroups, and homological methods.Updated on Oct 20, 2023 04:22 PM PDT -
Commutative Algebra and its Interaction with Algebraic Geometry
Organizers: Craig Huneke (University of Virginia), Sonja Mapes (University of Notre Dame), Juan Migliore (University of Notre Dame), LEAD Claudia Polini (University of Notre Dame), Claudiu Raicu (University of Notre Dame)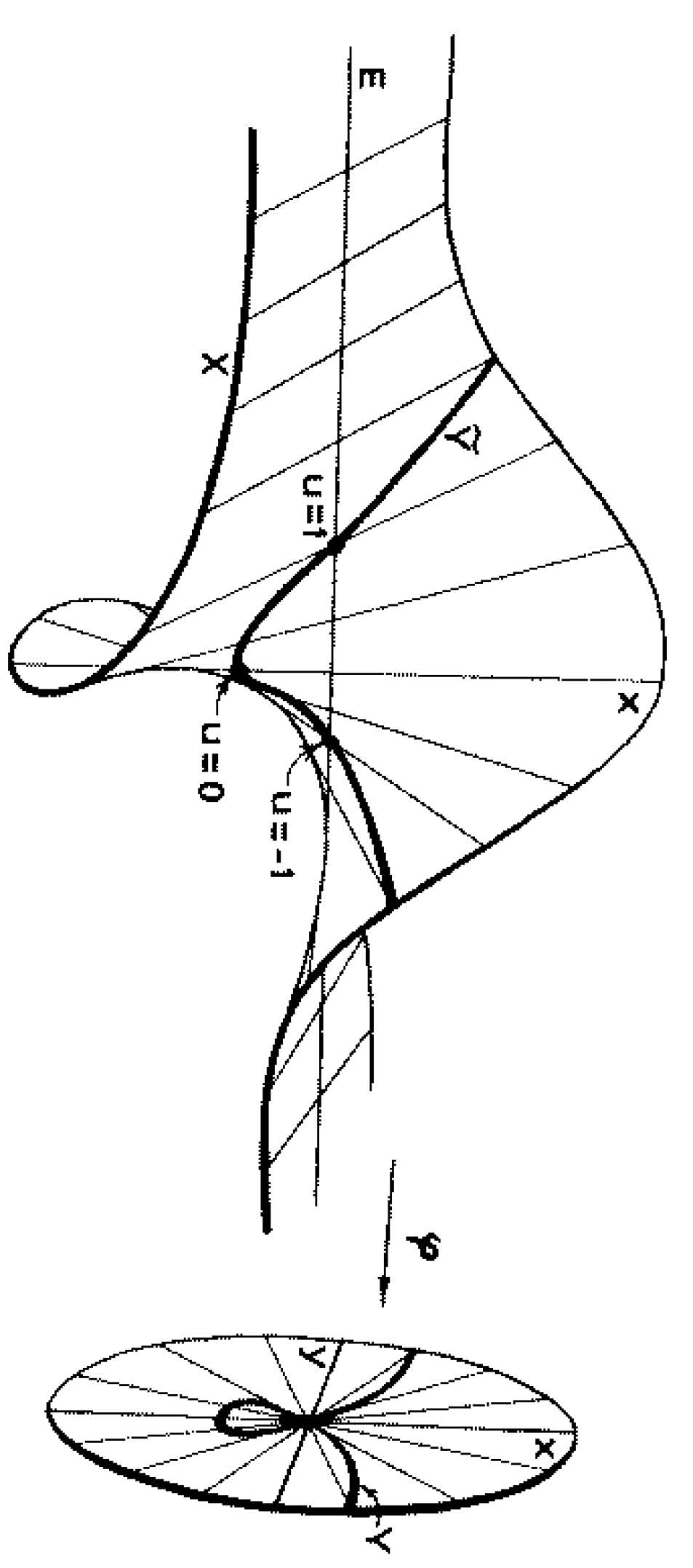 The figure represents a blow-up. The so called blow-up algebras or Rees rings are the algebraic realizations of such blow-ups.
The figure represents a blow-up. The so called blow-up algebras or Rees rings are the algebraic realizations of such blow-ups.Linkage is a method for classifying ideals in local rings. Residual intersections is a generalization of linkage to the case where the two `linked' ideals need not have the same codimension. Residual intersections are ubiquitous: they play an important role in the study of blowups, branch and multiple point loci, secant varieties, and Gauss images; they appear naturally in intersection theory; and they have close connections with integral closures of ideals.
Commutative algebraists have long used the Frobenius or p-th power map to study commutative rings containing a finite fi eld. The theory of tight closure and test ideals has widespread applications to the study of symbolic powers and to Briancon-Skoda type theorems for equi-characteristic rings.
Numerical conditions for the integral dependence of ideals and modules have a wealth of applications, not the least of which is in equisingularity theory. There is a long history of generalized criteria for integral dependence of ideals and modules based on variants of the Hilbert-Samuel and the Buchsbaum-Rim multiplicity that still require some remnants of finite length assumptions.
The Rees ring and the special fiber ring of an ideal arise in the process of blowing up a variety along a subvariety. Rees rings and special fiber rings also describe, respectively, the graphs and the images of rational maps between projective spaces. A difficult open problem in commutative algebra, algebraic geometry, elimination theory, and geometric modeling is to determine explicitly the equations defining graphs and images of rational maps.
The school will consist of the following four courses with exercise sessions plus a Macaulay2 workshop
- Linkage and residual intersections
- Characteristic p methods and applications
- Blowup algebras
- Multiplicity theory
Updated on May 29, 2019 09:11 AM PDT -
From Symplectic Geometry to Chaos
Organizers: Marcel Guardia (Polytechnical University of Cataluña (Barcelona) ), vadim kaloshin (University of Maryland), Leonid Polterovich (Tel Aviv University)The purpose of the summer school is to introduce graduate students to state-of-the-art methods and results in Hamiltonian systems and symplectic geometry. We focus on recent developments on the study of chaotic motion in Hamiltonian systems and its applications to models in Celestial Mechanics.
Updated on Jul 31, 2018 12:12 PM PDT -
Representations of High Dimensional Data
Organizers: Blake Hunter (Microsoft), Deanna Needell (University of California, Los Angeles) In today's world, data is exploding at a faster rate than computer architectures can handle. This summer school will introduce students to modern and innovative mathematical techniques that address this phenomenon. Hands-on topics will include data mining, compression, classification, topic modeling, large-scale stochastic optimization, and more.Updated on Jul 19, 2018 11:45 AM PDT
In today's world, data is exploding at a faster rate than computer architectures can handle. This summer school will introduce students to modern and innovative mathematical techniques that address this phenomenon. Hands-on topics will include data mining, compression, classification, topic modeling, large-scale stochastic optimization, and more.Updated on Jul 19, 2018 11:45 AM PDT -
IAS/PCMI 2018: Harmonic Analysis
Organizers: Carlos Kenig (University of Chicago), Fanghua Lin (New York University, Courant Institute), Svitlana Mayboroda (University of Minnesota, Twin Cities), Tatiana Toro (MSRI / Simons Laufer Mathematical Sciences Institute (SLMath))Harmonic analysis is a central field of mathematics with a number of applications to geometry, partial differential equations, probability, and number theory, as well as physics, biology, and engineering. The Graduate Summer School will feature mini-courses in geometric measure theory, homogenization, localization, free boundary problems, and partial differential equations as they apply to questions in or draw techniques from harmonic analysis. The goal of the program is to bring together students and researchers at all levels interested in these areas to share exciting recent developments in these subjects, stimulate further interactions, and inspire the new generation to pursue research in harmonic analysis and its applications.
Updated on Jun 20, 2018 12:17 PM PDT -
Derived Categories
Organizers: Nicolas Addington (University of Oregon), LEAD Alexander Polishchuk (University of Oregon)The goal of the school is to give an introduction to basic techniques for working with derived categories, with an emphasis on the derived categories of coherent sheaves on algebraic varieties. A particular goal will be to understand Orlov’s equivalence relating the derived category of a projective hypersurface with matrix factorizations of the corresponding polynomial.Updated on Jul 05, 2018 09:05 AM PDT -
H-principle
Organizers: Emmy Murphy (Princeton University), Takashi Tsuboi (RIKEN Interdisciplinary Theoretical and Mathematical Sciences Program) The image of a large sphere isometrically embedded into a small space through a C^1 embedding. (Attributions: E. Bartzos, V. Borrelli, R. Denis, F. Lazarus, D. Rohmer, B. Thibert)
The image of a large sphere isometrically embedded into a small space through a C^1 embedding. (Attributions: E. Bartzos, V. Borrelli, R. Denis, F. Lazarus, D. Rohmer, B. Thibert)This two week summer school will introduce graduate students to the theory of h-principles. After building up the theory from basic smooth topology, we will focus on more recent developments of the theory, particularly applications to symplectic and contact geometry, and foliation theory.
Updated on Jun 20, 2018 12:17 PM PDT -
Mathematical Analysis of Behavior
Organizers: Ann Hermundstad (Janelia Research Campus, HHMI), Vivek Jayaraman (Janelia Research Campus, HHMI), Eva Kanso (University of Southern California), L. Mahadevan (Harvard University)
Explore Outstanding Phenomena in Animal Behavior
Jointly hosted by Janelia and the Mathematical Sciences Research Institute (MSRI), this program will bring together 15-20 advanced PhD students with complementary expertise who are interested in working at the interface of mathematics and biology. Emphasis will be placed on linking behavior to neural dynamics and exploring the coupling between these processes and the natural sensory environment of the organism. The aim is to educate a new type of global scientist that will work collaboratively in tackling complex problems in cellular, circuit and behavioral biology by combining experimental and computational techniques with rigorous mathematics and physics.
Updated on Jun 20, 2018 12:16 PM PDT -
The ∂-Problem in the Twenty-First Century
Organizers: Debraj Chakrabarti (Central Michigan University), Jeffery McNeal (Ohio State University)This Summer Graduate School will introduce students to the modern theory of the inhomogeneous Cauchy-Riemann equation, the fundamental partial differential equation of Complex Analysis. This theory uses powerful tools of partial differential equations, differential geometry and functional analysis to obtain a refined understanding of holomorphic functions on complex manifolds. Besides students planning to work in complex analysis, this course will be valuable to those planning to study partial differential equations, complex differential and algebraic geometry, and operator theory. The exposition will be self-contained and the prerequisites will be kept at a minimum
Updated on Jun 21, 2018 01:13 PM PDT -
Séminaire de Mathématiques Supérieures 2018: Derived Geometry and Higher Categorical Structures in Geometry and Physics
Organizers: Anton Alekseev (Université de Genève), Ruxandra Moraru (University of Waterloo), Chenchang Zhu (Universität Göttingen)Higher categorical structures and homotopy methods have made significant influence on geometry in recent years. This summer school is aimed at transferring these ideas and fundamental technical tools to the next generation of mathematicians.
The summer school will focus on the following four topics: higher categorical structures in geometry, derived geometry, factorization algebras, and their application in physics. There will be eight to ten mini courses on these topics, including mini courses led by Chirs Brav, Kevin Costello, Jacob Lurie, and Ezra Getzler. The prerequisites will be kept at a minimum, however, a introductory courses in differential geometry, algebraic topology and abstract algebra are recommended.Updated on Jun 20, 2018 12:16 PM PDT -
Automorphic Forms and the Langlands Program
Organizers: LEAD Kevin Buzzard (Imperial College, London)The summer school will be an introduction to the more algebraic aspects of the theory of automorphic forms and representations. One of the goals will be to understand the statements of the main conjectures in the Langlands programme. Another will be to gain a good working understanding of the fundamental definitions in the theory, such as principal series representations, the Satake isomorphism, and of course automorphic forms and representations for groups such as GL_n and its inner forms.
Updated on Aug 04, 2017 11:02 AM PDT -
Nonlinear dispersive PDE, quantum many particle systems and the world between
Organizers: Natasa Pavlovic (University of Texas, Austin), Gigliola Staffilani (Massachusetts Institute of Technology), Nikolaos Tzirakis (University of Illinois at Urbana-Champaign)The purpose of the summer school is to introduce graduate students to the recent developments in the area of dispersive partial differential equations (PDE), which have received a great deal of attention from mathematicians, in part due to ubiquitous applications to nonlinear optics, water wave theory and plasma physics.
Recently remarkable progress has been made in understanding existence and uniqueness of solutions to nonlinear Schrodinger (NLS) and KdV equations, and properties of those solutions. We will outline the basic tools that were developed to address these questions. Also we will present some of recent results on derivation of NLS equations from quantum many particle systems and will discuss how methods developed to study the NLS can be relevant in the context of the derivation of this nonlinear equation.
Updated on Sep 12, 2017 02:02 PM PDT -
Séminaire de Mathématiques Supérieures 2017: Contemporary Dynamical Systems
Organizers: Sylvain Crovisier (Université de Paris VI (Pierre et Marie Curie)-Université de Paris XI (Paris-Sud)), LEAD Konstantin Khanin (University of Toronto), Andrés Navas Flores (University of Santiago de Chile), Christiane Rousseau (Université de Montréal), Marcelo Viana (Institute of Pure and Applied Mathematics (IMPA)), Amie Wilkinson (University of Chicago)The theory of dynamical systems has witnessed very significant developments in the last decades, including the work of two 2014 Fields medalists, Artur Avila and Maryam Mirzakhani. The school will concentrate on the recent significant developments in the field of dynamical systems and present some of the present main streams of research. Two central themes will be those of partial hyperbolicity on one side, and rigidity, group actions and renormalization on the other side. Other themes will include homogeneous dynamics and geometry and dynamics on infinitely flat surfaces (both providing connections to the work of Maryam Mirzakhani), topological dynamics, thermodynamical formalism, singularities and bifurcations in analytic dynamical systems.
Updated on May 06, 2017 01:18 AM PDT -
Positivity Questions in Geometric Combinatorics
Organizers: Eran Nevo (The Hebrew University of Jerusalem), Raman Sanyal (Johann Wolfgang Goethe-Universität Frankfurt)McMullen’s g-Conjecture from 1970 is a shining example of mathematical foresight that combined all results available at that time to conjure a complete characterization of face numbers of convex simple/simplicial polytopes. The key statement in its verification is that certain combinatorial numbers associated to geometric (or topological) objects are non-negative. The aim of this workshop is to introduce graduate students to selected contemporary topics in geometric combinatorics with an emphasis on positivity questions. It is fascinating that the dual notions of simple and simplicial polytopes lead to different but equally powerful algebraic frameworks to treat such questions. A key feature of the lectures will be the simultaneous development of these algebraic frameworks from complementary perspectives: combinatorial-topological and convex-geometric. General concepts (such as Lefschetz elements, Hodge–Riemann–Minkowski inequalities) will be developed side-by-side, and analogies will be drawn to concepts in algebraic geometry, Fourier analysis, rigidity theory and measure theory. This allows for entry points for students with varying backgrounds. The courses will be supplemented with guest lectures highlighting further connections to other fields.
Updated on Jul 21, 2017 10:13 AM PDT -
Soergel Bimodules
Organizers: LEAD Ben Elias (University of Oregon), Geordie Williamson (University of Sydney)We will give an introduction to categorical representation theory, focusing on the example of Soergel bimodules, which is a categorification of the Iwahori-Hecke algebra. We will give a comprehensive introduction to the "tool box" of modern (higher) representation theory: diagrammatics, homotopy categories, categorical diagonalization, module categories, Drinfeld center, algebraic Hodge theory.
Updated on Jul 10, 2017 01:18 PM PDT -
Subfactors: planar algebras, quantum symmetries, and random matrices
Organizers: LEAD Scott Morrison (Australian National University), Emily Peters (Loyola University), Noah Snyder (Indiana University)Subfactor theory is a subject from operator algebras, with many surprising connections to other areas of mathematics. This summer school will be devoted to understanding the representation theory of subfactors, with a particular emphasis on connections to quantum symmetries, fusion categories, planar algebras, and random matrices
Updated on Jun 20, 2017 03:34 PM PDT -
Commutative Algebra and Related Topics
Organizers: Shinobu Hikami (Okinawa Institute of Science and Technology), LEAD Shihoko Ishii (Tsinghua University), Kazuhiko Kurano (Meiji University), Ken-ichi Yoshida (Nihon University)The purpose of the school will be to introduce graduate students to foundational results in commutative algebra, with particular emphasis of the diversity of the related topics with commutative algebra. Some of these topics are developing remarkably in this decade and through learning those subjects the graduate students will be stimulated toward future research.
Updated on Jun 21, 2017 04:53 PM PDT -
Chip Firing and Tropical Curves
Organizers: LEAD Matthew Baker (Georgia Institute of Technology), David Jensen (University of Kentucky), Sam Payne (University of Texas, Austin)Tropical geometry uses a combination of techniques from algebraic geometry, combinatorics, and convex polyhedral geometry to study degenerations of algebraic varieties; the simplest tropical objects are tropical curves, which one can think of as "shadows" of algebraic curves. Linear equivalence of divisors on an abstract tropical curve is determined by a simple but rich combinatorial process called "chip firing", which was discovered independently in the discrete setting by physicists and graph theorists. From a pedagogical point of view, one can view tropical curves as a combinatorial model for the highly analogous but more abstract theory of algebraic curves, but there is in fact much more to the story than this: one can use tropical curves and chip firing to prove theorems in algebraic geometry and number theory. This field is relatively new, so participants will have the opportunity to start from scratch and still get a glimpse of the cutting edge in this active research area.
Updated on May 06, 2017 01:18 AM PDT -
Electronic Structure Theory
Organizers: LEAD Lin Lin (University of California, Berkeley), Jianfeng Lu (Duke University), James Sethian (University of California, Berkeley)Ab initio or first principle electronic structure theories, particularly represented by Kohn-Sham density functional theory (KS-DFT), have been developed into workhorse tools with a wide range of scientific applications in chemistry, physics, materials science, biology etc. What is needed are new techniques that greatly extend the applicability and versatility of these approaches. At the core, many of the challenges that need to be addressed are essentially mathematical. The purpose of the workshop is to provide graduate students a self-contained introduction to electronic structure theory, with particular emphasis on frontier topics in aspects of applied analysis and numerical methods.
Updated on May 06, 2017 01:18 AM PDT -
An Introduction to Character Theory and the McKay Conjecture
Organizers: Robert Guralnick (University of Southern California), Pham Tiep (Rutgers University)Character Theory of Finite Groups provides one of the most powerful tools to study groups. In this course we will give a gentle introduction to basic results in the Character Theory, as well as some of the main conjectures in Group Representation Theory, with particular emphasis on the McKay Conjecture.
Updated on May 06, 2017 01:18 AM PDT -
Mixed Integer Nonlinear Programming: Theory, algorithms and applications
Organizers: Francisco Castro (University of Sevilla), Elena Fernandez (Polytechnical University of Cataluña (Barcelona) ), Justo Puerto (University of Sevilla)This school is oriented to the presentation of theory, algorithms and applications for the solution of mixed integer nonlinear problems (MINLP). This type of problems appears in numerous application areas where the modelization of nonlinear phenomena with logical constraints is important; we must remember here the memorable phrase “the world is nonlinear”. Nowadays the theoretical aspects of this area are spread in a number of recent papers which makes it difficult, for non-specialist, to have a solid background of the existing results and new advances in the field. This school aims to organize and present this material in an organized way. Moreover, it also pursues to link theory with actual applications. In particular, remarkable applications can be found in air traffic control agencies, the air companies, the electric power generation companies, the chemical complex units, the analysis of financial products usually associated with risk dealing and in the algorithms in the statistical field and artificial intelligence as for instance artificial neural networks, or supporting vector machines, among many others.
Updated on May 06, 2017 01:18 AM PDT -
Harmonic Analysis and Elliptic Equations on real Euclidean Spaces and on Rough Sets
Organizers: LEAD Steven Hofmann (University of Missouri), Jose Maria Martell (Instituto de Ciencias Matematicas (ICMAT))The goal of the workshop is to present harmonic analysis techniques in $R^n$ (the ``flat" setting), and then to show how those techniques extend to much rougher settings, with application to the theory of elliptic equations. Thus, the subject matter of the workshop will introduce the students to an active, current research area: the interface between harmonic analysis, elliptic PDE, and geometric measure theory.
Updated on May 06, 2017 01:18 AM PDT -
Seminaire de Mathematiques Superieures 2016: Dynamics of Biological Systems
Organizers: Thomas Hillen (University of Alberta), Mark Lewis (University of Alberta), Yingfei Yi (University of Alberta)The purpose of this summer school is to focus on the interplay of dynamical and biological systems, developing the rich connectionbetween science and mathematics that has been so successful to date. Our focus will be on understanding the mathematical structure of dynamical systems that come from biological problems, and then relating the mathematical structures back to the biology to provide scientific insight. We will focus on five key areas: complex bio-networks, multi scale biological dynamics, biological waves, nonlinear dynamics of pattern formation, and disease dynamics. For each of the five key areas, we will invite 2-3 world leaders who are also excellent communicators to deliver a series of 2-4 one-hour lectures. We expect an average of eight hours of lecture per subject area, spread over approximately two weeks.
Updated on May 06, 2017 01:18 AM PDT -
Incompressible Fluid Flows at High Reynolds Number
Organizers: Jacob Bedrossian (University of Maryland), LEAD Vlad Vicol (New York University, Courant Institute)The purpose of this two week workshop is to introduce graduate students to state-of-the-art methods and results in mathematical fluid dynamics. In the first week, we will discuss the mathematical foundations and modern analysis aspects of the Navier-Stokes and Euler equations. In the second week, we will run two courses concurrently on the topics of inviscid limits and hydrodynamic stability. Specifically, one course will focus on boundary layers in high Reynolds number flows and the Prandtl equations while the other will focus on mixing and connections to turbulence. Through the lectures and associated problem sessions, the students will learn about a number of new analysis tools and principles of fluid mechanics that are not always taught in a graduate school curriculum.
Updated on May 06, 2017 01:18 AM PDT -
Gaps between Primes and Analytic Number Theory
Organizers: Dimitris Koukoulopoulos (Université de Montréal), LEAD Emmanuel Kowalski (ETH Zurich), James Maynard (University of Oxford), Kannan Soundararajan (Stanford University)These courses will give students a full overview of the results of Zhang and Maynard on gaps between primes, and will provide them will a clear understanding of the tools involved. This will make accessible a significant part of modern analytic number theory. The lecturers will also make sure to include, within their course, examples and discussions going further than is strictly required to understand the proofs of Zhang and Maynard, e.g., in the direction of automorphic forms and the Riemann Hypothesis over finite fields.
Updated on May 06, 2017 01:18 AM PDT -
Berkeley summer course in mining and modeling of neuroscience data
Organizers: Ingrid Daubechies (Duke University), Bruno Olshausen (University of California, Berkeley), Christos Papadimitriou (University of California, Berkeley), Fritz Sommer (University of California, Berkeley), LEAD Jeff Teeters (University of California, Berkeley)This course is for students and researchers with backgrounds in mathematics and computational sciences who are
interested in applying their skills toward problems in neuroscience. It will introduce the major open questions of
neuroscience and teach state-of–the-art techniques for analyzing and modeling neuroscience data sets. The course is designed for students at the graduate level and researchers with background in a quantitative field such as
engineering, mathematics, physics or computer science who may or may not have a specific neuroscience
background. The goal of this summer course is to help researchers find new exciting research areas and at the same time to strengthen quantitative expertise in the field of neuroscience. The course is sponsored by the National Science Foundation from a grant supporting activities at the data sharing repository CRCNS.org, the Helen Wills
Neuroscience Institute, the Simons Institute for the Theory of Computing and the Mathematical Science Research
Institute.Updated on May 06, 2017 01:18 AM PDT -
Mathematical Topics in Systems Biology
Organizers: LEAD Steven Altschuler (University of California, San Francisco), Lani Wu (University of California, San Francisco)This Summer Graduate School will introduce mathematics graduate students to the rapidly emerging area of systems biology. In particular, we will focus on the design and emergent behaviors of molecular networks used by cells to interpret their environments and create robust temporal-spatial behaviors. This will be a very hands-on workshop with students working alone and in teams to program and present key ideas.
Updated on May 06, 2017 01:18 AM PDT -
NIMS Summer School on Random Matrix Theory
Organizers: LEAD Jinho Baik (University of Michigan)This summer graduate school will take place at the National Institute for Mathematical Sciences in Daejeon, South Korea. The purpose of this summer school is to introduce some of the basic ideas and methods of random matrix theory to graduate students. In particular there will be three lecture series on random matrix theory from three different perspectives: from the view points of the integrable structures, the moment method, and the Stieltjes transorm technique. In addition to the lectures, there will be discussion sessions, and the students will also have plenty of time to interact with the lecturers and with other students.
Please note that accepted students will be provided up to $1700 in travel reimbursement, in addition to meals and accommodation.
Updated on May 06, 2017 01:18 AM PDT -
Seminaire de Mathematiques Superieures 2015: Geometric and Computational Spectral Theory
Organizers: Alexandre Girouard (Laval University), Dmitry Jakobson (McGill University), Michael Levitin (University of Reading), Nilima Nigam (Simon Fraser University), Iosif Polterovich (Université de Montréal), Frederic Rochon (Université du Québec à Montréal)The lectures will focus on the following four topics: geometry of eigenvalues, geometry of eigenfunctions, spectral theory on manifolds with singularities and computational spectral theory. There has been a number of remarkable recent developments in these closely related fields. The goal of the school is to shed light on different facets of modern spectral theory and to provide a unique opportunity for graduate students and young researchers to get a “big picture” of this rapidly evolving area of mathematics. A particularly novel aspect of the school is the emphasis on the interactions between spectral geometry and computational spectral theory.
Updated on May 06, 2017 01:18 AM PDT -
Geometric Group Theory
Organizers: LEAD John Mackay (University of Bristol), Anne Thomas (University of Sydney), Kevin Wortman (University of Utah)The aim of this workshop is to introduce graduate students to some specific core topics which will be under study at the upcoming MSRI program on Geometric Group Theory (GGT) in 2016. GGT encompasses a wide range of topics. The four minicourse topics have been chosen because they are central themes in GGT and in the upcoming MSRI program. Moreover, each topic is accessible to students with a range of backgrounds: the basic definitions are straightforward, with many simple and illuminating examples to work through, yet lead through to important questions in current research.
Updated on May 06, 2017 01:18 AM PDT -
CRM-PIMS Summer School in Probability
Organizers: LEAD Louigi Addario-Berry (McGill University), Louis-Pierre Arguin (University of Montreal), Alexander Fribergh (University of Montreal), Lea Popovic (Concordia University)The 2015 CRM-PIMS Summer School in Probability will take place in Montreal, Canada, from June 15-July 11, 2015. The school is built around two principal 24-hour lecture courses, which will be delivered by Alice Guionnet (random matrices, free probability and the enumeration of maps) and Remco van der Hofstad (high-dimensional percolation and random graphs). There will additionally be mini-courses by Louigi Addario-Berry (random minimum spanning trees), Shankar Bhamidi (dynamic random network models) and Jonathan Mattingly (stabilization by noise). Some time is reserved for participants to present their own work.
Updated on May 06, 2017 01:18 AM PDT -
Geometry and Analysis
Organizers: Hans-Joachim Hein (Imperial College, London), LEAD Aaron Naber (Northwestern University)Geometric and complex analysis is the application of tools from analysis to study questions from geometry and topology. This two week summer course will provide graduate students with the necessary background to begin studies in the area. The first week will consist of introductory courses on geometric analysis, complex analysis, and Riemann surfaces. The second week will consist of more advanced courses on the regularity theory of Einstein manifolds, Kahler-Einstein manifolds, and the analysis of Riemann surfaces.
Updated on May 06, 2017 01:18 AM PDT -
Stochastic Partial Differential Equations
Organizers: Yuri Bakhtin (New York University, Courant Institute), LEAD Ivan Corwin (Columbia University), James Nolen (Duke University)Stochastic Partial Differential Equations (SPDEs) serve as fundamental models of physical systems subject to random inputs, interactions or environments. It is a particular challenge to develop tools to construct solutions, prove robustness of approximation schemes, and study properties like ergodicity and fluctuation statistics for a wide variety of SPDEs.
The purpose of this two week workshop is to educate graduate students on the state-of-the-art methods and results in SPDEs. The three courses which will be run simultaneously will highlight different (though related) aspects of this area including (1) Fluctuation theory of PDEs with random coefficients (2) Ergodic theory of SPDEs and (3) Exact solvability of SPDEsUpdated on May 01, 2019 02:31 PM PDT -
Algebraic Topology
Organizers: LEAD Jose Cantarero-Lopez (Centro de Investigación en Matemáticas), LEAD Michael Hill (University of California, Los Angeles)Modern algebraic topology is a broad and vibrant field which has seen recent progress on classical problems as well as exciting new interactions with applied mathematics. This summer school will consist of a series of lecture by experts on major research directions, including several lectures on applied algebraic topology. Participants will also have the opportunity to have guided interaction with the seminal texts in the field, reading and speaking about the foundational papers.
Videos of selected lectures may be found here.
Updated on May 06, 2017 01:18 AM PDT -
IAS/PCMI 2014: Mathematics and Materials
Organizers: Mark Bowick (Syracuse University), David Kinderlehrer (Carnegie Mellon University), Govind Menon (Brown University), Charles Radin (University of Texas)The program in 2014 will bring together a diverse group of mathematicians and scientists with interests in fundamental questions in mathematics and the behavior of materials. The meeting addresses several themes including computational investigations of material properties, the emergence of long- range order in materials and self-assembly, the geometry of soft condensed matter and the calculus of variations, phase transitions and statistical mechanics. The program will cover several topics in discrete and differential geometry that are motivated by questions in materials science. Many central topics, such as the geometry of packings, problems in the calculus of variations and phase transitions, will be discussed from the complementary points of view of mathematicians and physicists.
Updated on May 06, 2017 01:18 AM PDT -
Seminaire de Mathematiques Superieures 2014: Counting Arithmetic Objects
Organizers: Henri Darmon (McGill University), Andrew Granville (Université de Montréal), Benedict Gross (Harvard University)Updated on May 06, 2017 01:18 AM PDT -
Dispersive Partial Differential Equations
Organizers: Natasa Pavlovic (University of Texas, Austin), Nikolaos Tzirakis (University of Illinois at Urbana-Champaign)The purpose of the workshop is to introduce graduate students to the recent developments in the area of dispersive partial differential equations (PDE).
Dispersive equations have received a great deal of attention from mathematicians because of their applications to nonlinear optics, water wave theory and plasma physics. We will outline the basic tools of the theory that were developed with the help of multi-linear Harmonic Analysis techniques. The exposition will be as self-contained as possible.
Updated on May 01, 2019 02:26 PM PDT -
Introduction to the Mathematics of Seismic Imaging
Organizers: LEAD Gunther Uhlmann (University of Washington)In this two week program we will develop some of the mathematical foundations of seismic imaging that is a basic tool used in ``Imaging the Earth Interior". This is one of the components of the Mathematics of Planet Earth year in 2013.
The goal in seismic imaging is to determine the inner structure of the Earth from the crust to the inner core by using information provided by earthquakes in the case of the deep interior or by measuring the reflection of waves produced by acoustic or elastic sources on the surface of the Earth. The mathematics of seismic imaging involves solving inverse problems for the wave equation. No previous experience on inverse problems will be assumed.
Updated on Aug 16, 2019 01:33 PM PDT -
Mathematical General Relativity in Cortona, Italy
Organizers: Justin Corvino (Lafayette College), Pengzi Miao (University of Miami), Giorgio Patrizio (Istituto Nazionale di Alta Matematica "Francesco Severi" (INdAM))In cooperation with INdAM (Istituto Nazionale di Alta Matematica) and the CMI (Clay Mathematical Institute), MSRI will sponsor a summer graduate workshop on Mathematical General Relativity in Cortona during the summer of 2013; the school will reprise the very successful school of Mathematical General Relativity held at MSRI in 2012.
Mathematical general relativity is the study of mathematical problems related to Einstein's theory of gravitation. There are interesting connections between the physical theory and problems in differential geometry and partial differential equations.
The purpose of the summer school is to introduce graduate students to some fundamental aspects of mathematical general relativity, with particular emphasis on the geometry of the Einstein constraint equations and the Positive Mass Theorem. These topics will comprise a component of the upcoming semester program at MSRI in Fall 2013.
There will be mini-courses, as well as several research lectures.
Updated on May 06, 2017 01:18 AM PDT -
New Geometric Techniques in Number Theory
Organizers: Toby Gee (Imperial College, London), LEAD Ariane Mézard (Institut de Mathématiques de Jussieu; École Normale Supérieure), David Nadler (University of California, Berkeley), Peter Scholze (Universität Bonn)The branches of number theory most directly related to automorphic forms have seen enormous progress over the past five years. Techniques introduced since 2008 have made it possible to prove many new arithmetic applications. The purpose of the current workshop is to drow the attention of young students or researchers to new questions that have arisen in the course of bringing several chapters in the Langlands program and related algebraic number theory to a close. We will focus especially on some precise questions of a geometric nature, or whose solutions seem to require new geometric insights. A graduate level in Number Theory is expected.
This two-week workshop will be devoted to the following subjects: Automorphy lifting theorems, p-adic local Langlands program, Characters of categorical representations and Hasse-Weil zeta function. During the first week, the lecturers present an open question and related mathematical objects. The first exercice sessions serve to direct the participants to an appropriate subject depending on their level. During the second week, the lecturers give some more advanced lectures on the field.
Updated on May 01, 2019 01:19 PM PDT -
IAS/PCMI Summer 2013: Geometric Analysis
Organizers: Hubert Bray (Duke University), Greg Galloway (University of Miami), Rafe Mazzeo (Stanford University), Natasa Sesum (Rutgers University)This Summer Graduate Workshop will be held in Park City, Utah.
The Graduate Summer School bridges the gap between a general graduate education in mathematics and the specific preparation necessary to do research on problems of current interest. In general, these students will have completed their first year, and in some cases, may already be working on a thesis. While a majority of the participants will be graduate students, some postdoctoral scholars and researchers may also be interested in attending.
We strongly recommend that graduate students have already had the equivalent of rigorous first year graduate-level courses in topology, algebra and analysis.
The main activity of the Graduate Summer School will be a set of intensive short lectures offered by leaders in the field, designed to introduce students to exciting, current research in mathematics. These lectures will not duplicate standard courses available elsewhere. Each course will consist of lectures with problem sessions. Course assistants will be available for each lecture series. The participants of the Graduate Summer School meet three times each day for lectures, with one or two problem sessions scheduled each day as well.
Updated on May 06, 2017 01:18 AM PDT -
Seminaire de Mathematiques Superieures 2013: Physics and Mathematics of Link Homology
Organizers: Sergei Gukov (California Institute of Technology), Mikhail Khovanov (Columbia University), Johannes Walcher (McGill University)This Summer Graduate Workshop will be held in Montreal, Canada.
Homology theories of knots and links is a burgeoning field at the interface of mathematics with theoretical physics. The 2013 edition of the SMS will bring together leading researchers in mathematics and mathematical physics working in this area, with the aim to educate a new generation of scientists in this exciting subject. The school will provide a pedagogical review of the current state of the various constructions of knot homologies, and also encourage interactions between the communities in order to facilitate development of the unified picture.
Updated on May 06, 2017 01:18 AM PDT -
Algebraic Topology
Organizers: Andrew Blumberg (Columbia University), Teena Gerhardt (Michigan State University), LEAD Michael Hill (University of California, Los Angeles)Modern algebraic topology is a broad and vibrant field which has seen recent progress on classical problems as well as exciting new interactions with applied mathematics. This summer school will consist of a series of lecture by experts on major research directions, including several lectures on applied algebraic topology. Participants will also have the opportunity to have guided interaction with the seminal texts in the field, reading and speaking about the foundational papers.
Updated on May 06, 2017 01:18 AM PDT -
Model Theory
Organizers: David Marker* (University of Illinois, Chicago), Thomas Scanlon (University of California, Berkeley), Carol Wood (Wesleyan University).The workshop will consist of two minicourses, together with a selection of topical lectures.
In the model theory course, o-minimality, and specifically the concrete example of the semi-algebraic sets of real numbers will provide the setting in which we introduce various fundamental results from model theory.
The algebraic dynamics course will allow the introduction of concepts and proof techniques from number theory and algebraic geometry in the context of applications involving model theory.Toward the end of the workshop, the two minicourses will converge on the Pila-Wilkie theorem concerning points on analytic varieties, a result crucial in recent applications of o-minimality to diophantine geometry.
Updated on Aug 09, 2023 08:34 AM PDT -
Mathematical General Relativity
Organizers: Justin Corvino* (Lafayette College) and Pengzi Miao (University of Miami)Mathematical general relativity is the study of mathematical problems related to Einstein's theory of gravitation. There are interesting connections between the physical theory and problems in differential geometry and partial differential equations.
The purpose of the workshop is to introduce graduate students to some fundamental aspects of mathematical general relativity, with particular emphasis on the geometry of the Einstein constraint equations and the Positive Mass Theorem. These topics will comprise a component of the upcoming semester program at MSRI in Fall 2013.
There will be mini-courses, as well as several research lectures. Students are expected to have had courses in graduate real analysis and Riemannian geometry, while a course in graduate-level partial differential equations is recommended.
Updated on Dec 11, 2023 11:53 AM PST -
IAS/PCMI Summer 2012: Geometric Group Theory
Organizers: Mladen Bestvina (University of Utah), Michah Sageev (Technion – Israel Institute of Technology), and Karen Vogtmann (Cornell University)This Summer Graduate Workshop will be held in Park City, Utah.
Some mobility between the Research in Mathematics and Graduate Summer School programs is expected and encouraged, but interested candidates should read the guidelines carefully and apply to the one program best suited to their field of study and experience. Postdoctoral scholars who are working in the field of Geometric Group Theory should apply to the Research Program in Mathematics, not to the Graduate Summer School.
Graduate students who are beyond their basic courses and recent PhDs in all fields of mathematics are encouraged to apply to the Graduate Summer School. Funding will go primarily to graduate students. Postdoctoral scholars not working in the field of Geometric Group Theory should also apply, but should be within four years of receipt of their PhD.
Deadline for submission of applications is January 31, 2012. Supplemental materials (such as Reference Letters) must be received in the PCMI office by February 4, 2012. Please plan accordingly. (Late applications may be accepted at the discretion of the organizers.) Response may be expected in early April. Financial support is available. Applicants are invited to request financial support by checking the appropriate boxes on the application form.Updated on Aug 09, 2023 08:34 AM PDT -
Seminaire de Mathematiques Superieures 2012: Probabilistic Combinatorics
Organizers: Louigi Addario-Berry* (McGill University), Luc Devroye (McGill University), Bruce Reed (McGill University)This Summer Graduate Workshop will be held in Montreal, Canada.
One of the cornerstones of the probabilistic approach to solving combinatorial problems is the following guiding principle: information about global structure can be obtained through local analysis. This principle is ubiquitous in probabilistic combinatorics. It arises in problems ranging from graph colouring, to Markov chain mixing times, to Szemerédi's regularity lemma and its applications, to the theory of influences. The 2012 Séminaire de Mathématiques Supérieures brings together experts in probabilistic combinatorics from around the world, to explain cutting edge research which in one way or another exhibits this principle.
Updated on Aug 09, 2023 08:34 AM PDT -
Noncommutative Algebraic Geometry
Organizers: Dan Rogalski* (University of California, San Diego), Travis Schedler (Massachusetts Institute of Technology), Michael Wemyss (The University of Edinburgh, United Kingdom)This workshop will introduce some of the major themes of the MSRI program "Interactions between Noncommutative Algebra, Representation Theory, and Algebraic Geometry" to be held in the spring of 2013. There will be four mini-courses on the topics of noncommutative projective geometry, deformation theory, noncommutative resolutions of singularities, and symplectic reflection algebras. As well as providing theoretical background, the workshop will aim to equip participants with some intuition for the many open problems in this area through worked examples and experimental computer calculations.
Updated on Apr 19, 2024 03:29 PM PDT -
Cluster Algebras and Cluster Combinatorics
Organizers: Gregg Musiker (University of Minnesota), Lauren Williams* (University of California, Berkeley)Cluster algebras are a class of combinatorially defined rings that provide a unifying structure for phenomena in a variety of algebraic and geometric contexts. A partial list of related areas includes quiver representations, statistical physics, and Teichmuller theory. This summer workshop for graduate students will focus on the combinatorial aspects of cluster algebras, thereby providing a concrete introduction to this rapidly-growing field. Besides providing background on the fundamentals of cluster theory, the summer school will cover complementary topics such as total positivity, the polyhedral geometry of cluster complexes, cluster algebras from surfaces, and connections to statistical physics. No prior knowledge of cluster algebras will be assumed.
The workshop will consist of four mini-courses with accompanying tutorials. Students will also have opportunities for further exploration using computer packages in Java and Sage.
Updated on Aug 09, 2023 08:34 AM PDT -
Toric Varieties in Cortona, Italy
Organizers: Scientific Committee: David Cox* (Amherst College) and Hal Schenck (University of Illinois)
Organizing Committee: Giorgio Patrizio (Università di Firenze, Italy) and Sandro Verra (Università di Roma Tre, Italy)In cooperation with INdAM (Istituto Nazionale di Alta Matematica) and the SMI (Scuola Matematica Interuniversitaria), MSRI will sponsor a summer graduate workshop (SGW) on toric varieties in Cortona during summer of 2011; the workshop will reprise the very successful SGW on toric varieties held at MSRI in 2009.
Toric varieties are algebraic varieties defined by combinatorial data, and there is a wonderful interplay between algebra, combinatorics and geometry involved in their study. Many of the key concepts of abstract algebraic geometry (for example, constructing a variety by glueing affine pieces) have very concrete interpretations in the toric case, making toric varieties an ideal tool for introducing students to abstruse concepts.Special restrictions apply, please see the workshop homepage.
Updated on Aug 09, 2023 08:34 AM PDT -
Geometric Measure Theory and Applications
Organizers: Camillo De Lellis (Universität Zürich), Tatiana Toro* (University of Washington)Geometric Measure Theory (GMT) is a field of Mathematics that has contributed greatly to the development of the calculus of variations and geometric analysis. In recent years it has experienced a new boom with the development of GMT in the metric space setting which has lead to unexpected applications (for examples to questions arising from theoretical computer sciences). The goal of this summer graduate workshop is to introduce students to different aspects of this field. There will be 5 mini-courses and a couple of research lectures. We expect students to have a solid background in measure theory.
Updated on Mar 04, 2024 02:03 PM PST -
IAS-PCMI Summer School on Moduli Spaces of Riemann Surfaces
Organizers: Benson Farb (University of Chicago), Richard Hain (Duke University), and Eduard Looijenga (University of Utrecht, Netherlands)The study of moduli spaces of Riemann surface is a rich mixture of geometric topology, algebraic topology, complex analysis and algebraic geometry. Each community of researchers that studies these moduli spaces generates its own problems and its own techniques for solving them. However, it is not uncommon for researchers in one community to solve problems generated by another once they become aware of them. The goal of this summer school is to give graduate students a broad background in the various approaches to the study of moduli spaces of Riemann surfaces so that they will be aware of the problems and techniques of many of the communities that study these fascinating objects. Graduate student participants from the various communities will be encouraged to interact with their colleagues from the other communities of students in order to maximize cross fertilization.
Special restrictions apply, please see the workshop homepage.
Updated on Aug 09, 2023 08:34 AM PDT -
Seminaire de Mathematiques Superieures 2011. Metric Measure Spaces: Geometric and Analytic Aspects.
Organizers: Galia Dafni* (Concordia University, Montreal), Robert McCann (University of Toronto), and Alina Stancu (Concordia University, Montreal)In cooperation with the CRM (Centre de Recherches Mathematiques), the Fields Institute, and the PIMS (Pacific Insitute for Mathematical Sciences), MSRI will sponsor a summer graduate workshop on Metric measure spaces: geometric and analytic aspects in Montreal, Canada.
In recent decades, metric-measure spaces have emerged as a fruitful source of mathematical questions in their own right, and as indispensable tools for addressing classical problems in geometry, topology, dynamical systems and partial differential equations. The purpose of the 2011 summer school is to lead young scientists to the research frontier concerning the analysis and geometry of metric-measure spaces, by exposing them to a series of mini-courses featuring leading researchers who will present both the state-of-the-art and the exciting challenges which remain.
Special restrictions apply, please see the workshop homepage.
Updated on Aug 09, 2023 08:34 AM PDT -
The Dirichlet Space: Connections between Operator Theory, Function Theory, and Complex Analysis
Organizers: Nicola Arcozzi (Universita' di Bologna), Richard Rochberg (Washington University), Eric T Sawyer (McMaster University), Brett D Wick* (Georgia Institute of Technology)This workshop will focus on the classical Dirichlet space of holomorphic functions on the unit disk. This space is at the center of several active, interrelated areas of research that, viewed more broadly, focus on the interaction between function theoretic operator theory and potential theory. There are several goals of this Summer Graduate Workshop. First, mathematically, the workshop will demonstrate the basic properties of the Dirichlet space, then introduce the technique of Trees in Function Spaces. The workshop will show the interconnections between the areas of Complex Analysis, Function Theory, and Operator Theory and will also illustrate the real-variable analogues of the analytic result discussed.
Updated on Aug 09, 2023 08:34 AM PDT -
Commutative Algebra
Organizers: Daniel Erman (Stanford University), Irena Swanson* (Reed College), and Amelia Taylor (Colorado College)This workshop will involve a combination of theory and symbolic computation in commutative algebra. The lectures are intended to introduce three active areas of research: Boij-Söderberg theory, algebraic statistics, and integral closure. The lectures will be accompanied with tutorials on the computer algebra system Macaulay 2.
Updated on Apr 23, 2024 10:17 AM PDT -
Algebraic, Geometric, and Combinatorial Methods for Optimization
Organizers: Matthias Köppe (University of California, Davis) and Jiawang Nie (University of California, San Diego)This workshop is intended to introduce to graduate students the main ideas of algebraic, geometric and combinatorial methods in global optimization. We emphasize the major developments in the past few years from two viewpoints. The first one is that of the interaction of semidefinite programming and real algebraic geometry and includes topics such as linear matrix inequalities, positive polynomials, and sums of squares. The second viewpoint is that of primal methods and generating function methods in integer linear and nonlinear optimization.
Updated on Aug 09, 2023 08:34 AM PDT -
Mathematics of Climate Change
Organizers: Chris Jones (University of North Carolina and University of Warwick), Doug Nychka (National Center for Atmospheric Research), and Mary Lou Zeeman (Bowdoin College)NCAR supports scientific research on nearly every aspect of the atmosphere and related components of the Earth’s physical and biological systems. This includes developing state-of-the- art climate models, high performance computing and also innovative ways of observing the atmosphere and oceans. The Center has approximately 1000 staff and is supported primarily by the National Science Foundation. Part of the NCAR mission is to engage students in the problems of understanding climate and weather and so provides an ideal context for this summer graduate workshop. The workshop is also part a larger program at NCAR through the Institute for Mathematics Applied to Geosciences: Mathematicians and Climate.
For more information, please see NCAR summer school pageUpdated on Aug 09, 2023 08:34 AM PDT -
IAS/PCMI Research Summer School 2010: Image Processing
Organizers: Tony Chan (University of California, Los Angeles), Ron Devore (Unversity of South Carolina, Columbia), Stanley Osher (University of California, Los Angeles), and Hongkai Zhao (University of California, Irvine)Both an MSRI nomination and PCMI application are required to attend the Image Processing summer school. The application form can be found by going to the PCMI page IAS/PCMI application homepage and clicking on the sentence "You're ready to apply."
Once the PCMI application is complete IAS/PCMI application homepage please return a letter of nomination from the Director of Graduate Studies to MSRI.Updated on Mar 05, 2024 03:44 PM PST -
Probability workshop: 2010 PIMS Summer School in Probability.
Organizers: Krzysztof Burdzy (University of Washington), Zhenqing Chen (University of Washington), Christopher Hoffman (University of Washington), Soumik Pal (University of Washington), Yuval Peres ( University of California, Berkeley)The 2010 Pacific Institute for the Mathematical Sciences (PIMS) Summer
School in Probability will be held at the University of Washington and
Microsoft Research. The workshop will have two main courses, and three short ones.For further information please visit the following link pims homepage
Updated on Aug 09, 2023 08:34 AM PDT -
Sage Days 22: Computing with Elliptic Curves
Organizers: William Stein (University of Washington)This workshop will introduce graduate students to several central ideas in the arithmetic of elliptic curves. Participants will join a project group that will focus mainly on one topic, possibly involving elliptic curves over number fields, complex or p-adic L-functions, Heegner points and Kolyvagin classes, Iwasawa theory, and the Birch and Swinnerton-Dyer conjecture. The workshop will emphasize the essential interplay of abstract mathematics with explicit computation, which has played a central role in number theory ever since Birch and Swinnerton-Dyer made their famous conjecture in the 1960s. Participants will use, and improve, the free open-source Python-based mathematical software system Sage (http://www.sagemath.org) for computational projects.
Updated on Aug 14, 2023 04:43 PM PDT -
Summer School on Operator Algebras and Noncommutative Geometry
Organizers: Heath Emerson, (University of Victoria) Thierry Giordano, (University of Ottawa) Marcelo Laca*, (University of Victoria) Ian Putnam, (University of Victoria)The summer school aims to expose participants to the classi cation of noncommutative
spaces, to the study of their homological and cohomological invariants, and to explore fascinating
new connections between their symmetries and long standing problems in number
theory. Additional information can be found on the PIMS pageUpdated on Aug 09, 2023 08:34 AM PDT -
Summer Graduate Workshop: Symplectic and Contact Geometry and Topology
Organizers: John Etnyre (Georgia Institute of Technology), Dusa McDuff* (Barnard College, Columbia University) and Lisa Traynor (Bryn Mawr College).Symplectic and Contact Topology has undergone rapid and exciting growth
in the past few decades and is currently a rich subject, employing a variety of diverse techniques and touching on many areas of mathematics, such as algebraic and differential geometry, dynamical systems and low dimensional topology. This workshop is intended both for graduate students new to the
area and for those working in the field.
Lectures in the first week will introduce participants to basic topological, geometric and analytic techniques, including J-holomorphic curves. The second week will discuss applications to symplectic geometry and to 3-dimensional topology and knot theory. A variety of discussion
sessions in the afternoon will cater to the differing interests of the students. Participants may consider staying for the Connections for Women and/or the Introductory workshop to the year long Symplectic Geometry program that starts just after this workshop.
Updated on Dec 13, 2023 10:52 AM PST -
Inverse Problems
Organizers: Gunther Uhlmann* (University of Washington).Inverse Problems are problems where causes for a desired or an observed effect are to be determined. They lie at the heart of scientific inquiry and technological development. Applications include a number of medical as well as other imaging techniques, location of oil and mineral deposits in the earth's substructure, creation of astrophysical images from telescope data, finding cracks and interfaces within materials, shape optimization, model identification in growth processes and, more recently, modelling in the life sciences.
The workshop will consist of several minicourses addressing several of the theoretical and practical issues arising in inverse problems including boundary rigidity and travel time tomography, cloaking and invisibility, electrical impedance imaging, statistical methods and biological applications, thermoacoustic and x-ray tomography, and resonances.
Updated on Aug 09, 2023 08:34 AM PDT -
Computational Theory of Real Reductive Groups (Salt lake City)
Organizers: Jeffrey Adams (University of Maryland) , Peter Trapa* (University of Utah), Susana Salamanca (New Mexico State University), John Stembridge (University of Michigan), and David Vogan (MIT).The structure of real reductive algebraic groups is controlled by a remarkably simple combinatorial framework, generalizing the presentation of Coxeter groups by generators and relations. This framework in turn makes much of the infinite-dimensional representation theory of such groups amenable to computation.
The Atlas of Lie Groups and Representations project is devoted to looking at representation theory from this computationally informed perspective. The group (particularly Fokko du Cloux and Marc van Leeuwen) has written computer software aimed at supporting research in the field, and at helping those who want to learn the subject.
The workshop will explore this point of view in lecture series aimed especially at graduate students and postdocs with only a modest background (such as the representation theory of compact Lie groups).
Deadline for funding applications: 1 March, 2009.
The official workshop website is at: http://www.liegroups.org/workshop/
Updated on Aug 09, 2023 08:34 AM PDT -
Random Matrix theory
Organizers: Jinho Baik ( University of Michigan), Percy Deift* (New York University),Toufic Suidan (University of Arizona), Brian Rider (University of Colorado)The goal of this workshop is two-fold: (1) to describe many of the recent advances that have been made in the application of random matrix theory to problems in mathematics and physics (2) to develop some of the mathematical tools that are needed to enter the field. Applications of random matrix theory are now being made to number theory, combinatorics, statistical physics and statistics amongst other fields. The techniques employed in the field include methods from integrable systems, combinatorics, complex analysis, orthogonal polynomials and of course random matrix theory per se.
Updated on Apr 10, 2023 12:18 PM PDT -
IAS/PCMI Summer Program: The Arithmetic of L-functions
Organizers: Cristian Popescu (UCSD), Karl Rubin ( UC Irvine) , Alice Silverberg (UC Irvine).For application forms and information please visit the following link IAS/PCMI application homepage
Updated on Aug 09, 2023 08:34 AM PDT -
Toric Varieties
Organizers: David Cox ( Amherst College) and Hal Schenck (University of Illinois)Toric varieties are algebraic varieties defined by combinatorial data, and there is a wonderful interplay between algebra, combinatorics and geometry involved in their study. Many of the key concepts of abstract algebraic geometry (for example, constructing a variety by gluing affine pieces) have very concrete interpretations in the toric case, making toric varieties an ideal tool for introducing students to abstruse concepts.
Updated on Apr 23, 2024 10:17 AM PDT -
Climate Change - Summer Graduate Workshop
Organizers: Christopher Jones (UNC Chapel Hill and U Warwick, UK), Inez Fung (U.C. Berkeley), Eric Kostelich (Arizona State University), K.K. Tung (U. Washington), and Mary Lou Zeeman (Bowdoin College), Charles D. Camp (Cal Poly, San Luis Obispo), Rachel Kuske (Univ British Columbia)The goal of the workshop will be to discern ways in which mathematics can contribute and to expose new researchers to some of the key areas that we believe will form the basis of serious mathematical considerations of climate change issues.
Updated on Dec 11, 2023 10:10 AM PST -
Geometry and Representation Theory of Tensors for Computer Science, Statistics, and other areas
Organizers: J.M. Landsberg (Texas A&M), Lek-Heng Lim (UC Berkeley) and Jason Morton (UC Berkeley)Recently the common geometry of tensors arising in questions in computational complexity, statistical learning theory, signal processing, scientific data analysis have been looked at from a unified perspective. The underlying geometry and representation theory will be covered in this workshop with and eye towards problems such as the complexity of matrix multiplication, Valiant's approach to P=NP, measures of entanglement in quantum information theory, graphicalmodels in statistical learning theory, independent component analysis and other multilinear data analytic techniques.
Updated on Feb 16, 2024 08:24 AM PST -
IAS/PCMI Summer Program: Analytic and Algebraic Geometry: Common Problems - Different Methods
Organizers: Mircea Mustaţă (University of Michigan), Jeff McNeal (Ohio State University)NOTE: This workshop requires a special application with a January 20, 2008 deadline. For application forms, please visit http://www.admin.ias.edu/ma/current/program_gradsummer.php
Updated on Aug 09, 2023 08:34 AM PDT -
A Window into Zeta and Modular Physics
Organizers: Floyd Williams (University of Massachusetts) and Klaus Kirsten (Baylor University)In recent years,a noteworthy and very fruitful interlacing of number theory and physics has emerged.As indicated in the September 2007 issue of the AMS Notices,for example,a new journal "Communications in Number Theory and Physics " has just been launched to follow significant interactions and dynamics between these two fields.Several books are now available,in addition to an array of conference and workshop activity,that accent this fortunate merger of "pure"mathematics and physical theory-with applications that range from field theory (conformal and topological),extended objects (strings and branes)cosmology and black hole physics, to Bose-Einstein condensation and the theory of relativistic gases.
Updated on Aug 09, 2023 08:34 AM PDT -
Deformation Theory and Moduli in Algebraic Geometry
Organizers: Max Lieblich (Princeton), Martin Olsson (Berkeley), Brian Osserman (Berkeley), Ravi Vakil (Stanford)This workshop is intended to introduce to graduate students the main ideas of deformation theory and moduli spaces in algebraic geometry. We hope to illuminate the general theory through extensive discussions of concrete examples and applications.
Updated on Jan 16, 2024 09:26 AM PST -
Continuous Optimization and Applications
Organizers: Henry Wolkowicz. (University of Waterloo)Updated on Aug 09, 2023 08:34 AM PDT -
Summer Graduate Workshop on Data Assimilation for the Carbon Cycle
Updated on Aug 09, 2023 08:34 AM PDT -
IAS/PCMI summer conference: Statistical Mechanics
Organizers: Scott Sheffield, Thomas SpencerUpdated on Aug 09, 2023 08:34 AM PDT -
Derived Categories in Algebraic Geometry
Organizers: Aaron Bertram (University of Utah), Y.P. Lee (university of Utah), Eric Sharpe (University of Utah and Virginia Tech)Updated on Feb 12, 2024 02:15 PM PST -
Summer Graduate Workshop in Computational Number Theory
Organizers: William Stein (University of Washington)This workshop will concentrate on computing with modular forms, providing students with the necessary background in both the theoretical and computational aspects of the subject.
Updated on Aug 09, 2023 08:34 AM PDT -
Data Assimilation for the Carbon Cycle
Organizers: Inez Fung (University of California, Berkeley)Projections of future climate require projections of the abundance of carbon dioxide and other trace constituents in the atmosphere. This in turns requires understanding the sources and sinks of atmospheric CO2 and how they interact with the climate. Participants will work on projects using atmospheric data provided by NCAR.
Updated on Aug 09, 2023 08:34 AM PDT -
IAS/PCMI Summer Program: Low Dimensional Topology
Organizers: Peter Oszvath (Columbia University) and Tom Mrowka (MIT).This will be a minicourse for graduate students on recent techniques and advances in three and four dimensional topology.
Updated on Aug 09, 2023 08:34 AM PDT -
MSRI Summer Graduate Workshop: Mathematical aspects of computational biology
Organizers: Reinhard Laubenbacher (Virginia Bioinformatics Institute at Virginia Tech) and Lior Pachter (Department of Mathematics, UC Berkeley)The novel features of biological systems pose new challenges that require new mathematics. In many cases even the fundamental mathematical language is lacking in order to treat certain biological phenomena quantitatively. Here, traditionally non-applied areas of mathematics can make an important contribution, and at the same time take advantage of unique new problems to open up mathematically interesting avenues of research.
Updated on Dec 11, 2023 10:10 AM PST -
SL(2,R), a Minicourse at the University of Utah
Organizers: Bill Casselman (University of British Columbia), Dragan Milicic (University of Utah), Peter Trapa (University of Utah)This minicourse will be aimed at beginning graduate students, and is devoted to all aspects of the theory of SL(2,R) including: discrete and principal series, intertwining operators, unitary representations, character theory, etc.
Updated on Aug 09, 2023 08:34 AM PDT -
Computing the Continuous Discretely: Integer Point Enumeration in Polyhedra (Summer Graduate Workshop)
Organizers: Mathias Beck and Sinai RobinsUpdated on Aug 09, 2023 08:34 AM PDT -
CR Geometry: Complex Analysis Meets Real Geometry and Number Theory
Organizers: John D’AngeloUpdated on Dec 13, 2023 10:28 AM PST -
AMS-IMS-SIAM Summer School in Commutative Algebra: Local Cohomology and Its Applications
Organizers: Anurag Singh and Uli WaltherGraduate Students from MSRI Sponsoring Institutions may benominated to participate in this program.
Updated on Aug 09, 2023 08:34 AM PDT -
Clay Mathematics Institute 2005 Summer School Ricci Flow, 3 Manifolds And Geometry
Organizers: Gang Tian, John Lott, John Morgan, Bennett Chow, Tobias Colding, Jim Carlson, David Ellwood, Hugo RossiGraduate Students from MSRI Sponsoring Institutions may benominated to participate in this program.
Updated on Mar 04, 2024 10:31 AM PST -
Mathematical Graphics
Organizers: David Austin, Bill Casselman and Jim FixUpdated on Aug 09, 2023 08:34 AM PDT -
Graduate Student Warm-Up Workshop in Algebraic Geometry
Organizers: Sándor Kovács, Tony Pantev, and Ravi VakilGraduate Students from MSRI Sponsoring Institutions may benominated to participate in this program.
Updated on Aug 09, 2023 08:34 AM PDT -
Knot Theory and 3-Manifolds (Summer Graduate Workshop)
Organizers: S. Boyer (UQAM), R. Fenn (Sussex), D. Rolfsen, Chair (UBC), D. Sjerve (UBC)Updated on Aug 09, 2023 08:34 AM PDT -
Hyperplane Arrangements and Applications
Organizers: Sergey YuzvinskyThis MSRI Summer Graduate Program at the University of Oregon will provide an introduction to the material to be covered in the fall, 2004 MSRI program on Hyperplane Arrangements and Applications. See the program page for more information on the content.
Updated on Aug 09, 2023 08:34 AM PDT -
Triangulations of Point Sets: Applications, Structures, Algorithms
Organizers: Jesús A. De Loera, Jörg Rambau, and Francisco SantosPlease note, MSRI's Summer Graduate Programs are open only to students nominated by MSRI's Academic Sponsor universities.
Updated on May 13, 2013 11:00 PM PDT -
Mathematical Graphics
Organizers: Bill Casselman and David AustinPlease note, MSRI's Summer Graduate Programs are open only to students nominated by MSRI's Academic Sponsor universities.
Updated on Aug 09, 2023 08:34 AM PDT -
Biomathematics, Bioengineering & Clinical Aspects of Blood Flow
Organizers: Stanley A. Berger, Giovanni P. Galdi (co-chair), Charles S. Peskin, Alfio Quarteroni, Anne M. Robertson (co-chair), Adélia Sequeira, and Howard YonasSummer Graduate Program -- open only to students nominated by MSRI's Academic Sponsor universities.
Updated on Aug 09, 2023 08:34 AM PDT -
Excursions in Computational Number Theory -- Polynomials with Integer Coefficients
Organizers: Peter Borwein and Michael FilasetaSummer Graduate Program -- open only to students nominated by MSRI's Academic Sponsor universities, to be held in Vancouver, BC, Canada at the Pacific Institute of Mathematics facility of Simon Fraser University.
Updated on Aug 09, 2023 08:34 AM PDT -
Combinatorial Game Theory (Summer Graduate Workshop II)
Organizers: Elwyn Berlekamp and David WolfeUpdated on Aug 09, 2023 08:34 AM PDT -
MSRI/PMMB Short Course: Mathematical and Computational Challenges in Molecular and Cell Biology
Organizers: Nicholas R. Cozzarelli, Michael Levitt, Wilma Olson, De Witt SumnersUpdated on Aug 09, 2023 08:34 AM PDT -
Lie groups and the method of the moving frame
Organizers: Robert Bryant and Jeanne N. ClellandUpdated on Aug 09, 2023 08:34 AM PDT -
Lie groups and the method of the moving frame / Exterior Differential Systems
Organizers: Jeanne N. Clelland and Robert Bryant,For more information, please see this programs original web page at http://www.msri.org/activities/events/9899/sgp99/bryant.html
Updated on Oct 12, 2018 02:29 PM PDT -
Summer Graduate Workshop in Nonlinear dynamics of low-dimensional continua
Organizers: Anette Hosoi and L. MahadevanUpdated on Aug 09, 2023 08:34 AM PDT -
Algorithmic Algebra and Geometry
Organizers: David Bayer, Sorin PopescuUpdated on Oct 12, 2018 02:38 PM PDT -
Cryptography
Organizers: Neal Koblitz, Alfred MenezesUpdated on Aug 09, 2023 08:34 AM PDT -
Algebra, Algorithms, and Approximation
Organizers: Dave Bayer, Ilan Vardi, John StrainUpdated on Aug 09, 2023 08:34 AM PDT -
Random Walk and Geometry
Organizers: Persi Diaconis, Laurent Saloff-CosteUpdated on Aug 09, 2023 08:34 AM PDT -
Hyperbolic Geometry
Organizers: William P. Thurston, Jane Gilman, David EpsteinUpdated on Aug 09, 2023 08:34 AM PDT -
Automorphic Forms and Zeta Functions
Organizers: Dan Bump, Dinakar RamakrishnanUpdated on Aug 09, 2023 08:34 AM PDT -
Mathematical Biology
Organizers: N. Kopell, C. Peskin, M. Reed (chairman), J. RinzelUpdated on Aug 09, 2023 08:34 AM PDT -
4-Manifolds
Organizers: Rob Kirby, Ron SternUpdated on Aug 09, 2023 08:34 AM PDT -
Computing the Continuous Discretely: Integer Point Enumeration in Polyhedra (Summer Graduate Program)
Organizers: Mathias Beck and Sinai RobinsUpdated on Oct 25, 2016 10:05 AM PDT -
CR Geometry: Complex Analysis Meets Real Geometry and Number Theory
Organizers: John D’AngeloUpdated on Oct 25, 2016 10:06 AM PDT -
Clay Mathematics Institute 2005 Summer School Ricci Flow, 3 Manifolds And Geometry
Organizers: Gang Tian, John Lott, John Morgan, Bennett Chow, Tobias Colding, Jim Carlson, David Ellwood, Hugo RossiGraduate Students from MSRI Sponsoring Institutions may benominated to participate in this program.
Updated on Oct 25, 2016 10:06 AM PDT -
Mathematical Graphics (Summer Graduate Program)
Organizers: David Austin, Bill Casselman and Jim FixUpdated on Oct 25, 2016 10:06 AM PDT -
AMS-IMS-SIAM Summer School in Commutative Algebra: Local Cohomology and Its Applications
Organizers: Anurag Singh and Uli WaltherGraduate Students from MSRI Sponsoring Institutions may benominated to participate in this program.
Updated on Oct 25, 2016 10:04 AM PDT -
Graduate Student Warm-Up Workshop in Algebraic Geometry
Organizers: Sándor Kovács, Tony Pantev, and Ravi VakilGraduate Students from MSRI Sponsoring Institutions may benominated to participate in this program.
Updated on Oct 25, 2016 10:05 AM PDT -
Summer Graduate Program in Hyperplane Arrangements and Applications (Summer Graduate Program)
Organizers: Sergey YuzvinskyThis MSRI Summer Graduate Program at the University of Oregon will provide an introduction to the material to be covered in the fall, 2004 MSRI program on Hyperplane Arrangements and Applications. See the program page for more information on the content.
Updated on Oct 25, 2016 09:57 AM PDT -
SGP: Knot Theory and 3-Manifolds
Organizers: Steven Boyer, Roger A Fenn and Dale RolfsenOpen only to graduate students nominated by MSRI's Academic Sponsors.
Updated on Oct 25, 2016 09:57 AM PDT -
SGP: Analysis of Algorithms
Organizers: P. Flajolet, G. Seroussi, W. Szpankowski, and M. WeinbergerPlease note, MSRI's Summer Graduate Programs are open only to students nominated by MSRI's Academic Sponsor universities.
Updated on Oct 25, 2016 09:57 AM PDT -
SGP: Triangulations of Point Sets: Applications, Structures, Algorithms
Organizers: Jesús A. De Loera, Jörg Rambau, and Francisco SantosPlease note, MSRI's Summer Graduate Programs are open only to students nominated by MSRI's Academic Sponsor universities.
Updated on Oct 25, 2016 09:57 AM PDT -
SGP: Mathematical Graphics
Organizers: Bill Casselman and David AustinPlease note, MSRI's Summer Graduate Programs are open only to students nominated by MSRI's Academic Sponsor universities.
Updated on Oct 25, 2016 09:56 AM PDT -
SGP: Biomathematics, Bioengineering & Clinical Aspects of Blood Flow
Organizers: Stanley A. Berger, Giovanni P. Galdi (co-chair), Charles S. Peskin, Alfio Quarteroni, Anne M. Robertson (co-chair), Adélia Sequeira, and Howard YonasSummer Graduate Program -- open only to students nominated by MSRI's Academic Sponsor universities.
Updated on Oct 25, 2016 09:56 AM PDT -
SGP: Excursions in Computational Number Theory -- Polynomials with Integer Coefficients
Organizers: Peter Borwein and Michael FilasetaSummer Graduate Program -- open only to students nominated by MSRI's Academic Sponsor universities, to be held in Vancouver, BC, Canada at the Pacific Institute of Mathematics facility of Simon Fraser University.
Updated on Oct 25, 2016 09:55 AM PDT -
SGP: The Global Theory of Minimal Surfaces
Organizers: Joel Hass and David HoffmanMSRI's second Graduate Summer Program for 2001.
Updated on Oct 25, 2016 09:55 AM PDT -
SGP: Modern Signal Processing
Organizers: Dan Rockmore and Dennis HealyMSRI's Summer Graduate Program I This summer graduate program, organized by Dan Rockmore and Dennis Healy, Jr., will introduce students to the world of signal processing. The course will cover standard tools of digital signal processing, but will also cover the exciting frontiers of the subject, including wavelets, ISP (integrated sensing and processing), image processing algorithms, etc. In addition, students will be briefly exposed to applications in various areas, such as biology, chemistry, medicine, music, and engineering.
Updated on Oct 25, 2016 09:55 AM PDT -
SGP: Combinatorial Game Theory
Organizers: E. Berlekamp, D. WolfeSUMMER GRADUATE PROGRAMFor more information about this program, please see the original web page at:http://www.msri.org/calendar/sgp/sgp2/index.html
Updated on Oct 25, 2016 09:54 AM PDT -
SGP: Mathematical and Computational Challenges In Molecular and Cell Biology
Organizers: Nicholas R. Cozzarelli, Michael Levitt, Wilma Olson, De Witt SumnersSUMMER GRADUATE PROGRAMFor more information about this program, please see the original web page at:http://www.msri.org/calendar/workshops/9900/Molecular_and_Cell_Biology/index.html
Updated on Oct 25, 2016 09:54 AM PDT -
SGP: Lie groups and the method of the moving frame / Exterior Differential Systems
Organizers: Jeanne N. Clelland and Robert Bryant,For more information, please see this programs original web page at http://www.msri.org/activities/events/9899/sgp99/bryant.html
Updated on Oct 25, 2016 09:54 AM PDT -
SGP: Nonlinear dynamics of low-dimensional continua
Organizers: L. Mahadevan and Anette HosoiFor more information, please see the original program page at http://www.msri.org/activities/events/9899/sgp99/mahadevan.html
Updated on Oct 25, 2016 09:53 AM PDT -
SGP: Algorithmic Algebra and Geometry
Organizers: David Bayer, Sorin PopescuUpdated on Oct 25, 2016 09:53 AM PDT -
SGP: Cryptography
Organizers: Neal Koblitz, Alfred MenezesUpdated on Oct 25, 2016 09:53 AM PDT -
SGP: Algebra, Algorithms, and Approximation
Organizers: Dave Bayer, Ilan Vardi, John StrainUpdated on Oct 25, 2016 09:52 AM PDT -
SGP: Random Walk and Geometry
Organizers: Persi Diaconis, Laurent Saloff-CosteUpdated on Oct 25, 2016 09:52 AM PDT -
SGP: Hyperbolic Geometry
Organizers: William P. Thurston, Jane Gilman, David EpsteinUpdated on Oct 25, 2016 09:51 AM PDT -
SGP: Automorphic Forms and Zeta Functions
Organizers: Dan Bump, Dinakar RamakrishnanUpdated on Oct 25, 2016 09:49 AM PDT -
SGP: Mathematical Biology
Organizers: N. Kopell, C. Peskin, M. Reed (chairman), J. RinzelUpdated on Oct 25, 2016 09:48 AM PDT -
SGP: 4-Manifolds
Organizers: Rob Kirby, Ron SternUpdated on Oct 25, 2016 09:32 AM PDT
