The Julia Robinson Mathematics Festivals are a program of in-person math events supplemented by deep contest problems you can work on in small teams at your school. Learn more at www.jrmf.org.
Julia Robinson was a mathematics professor at the University of California, Berkeley for many years. She is famous for her solution of Hilbert’s tenth problem. The Julia Robinson Mathematics Festivals were founded by MSRI in collaboration with Nancy Blachman, David desJardins and Joshua Zucker to honor her legacy and encourage more students to pursue mathematics. The festivals began in the San Francisco Bay Area in 2007 and have expanded with festivals across the country.

Nancy Blachman shares the history of the festival:
I have fond memories of working on qualifying problem sets for the Saint Mary’s Math Contest when I was in high school in Palo Alto during the 1970s. Every two months or so, my math teacher would give interested students a problem set from Saint Mary’s College in Moraga, California. The first few problems were usually pretty straightforward and easy, and solving one would boost my confidence in tackling the next. Students who received sufficient points on the year’s qualifying problems were invited to the Saint Mary’s Math Contest towards the end of the school year. Many schools in the San Francisco Bay Area took busloads of students to the contest. Sample problems from the contest are available here.
Working on the Saint Mary’s Math Contest problems was one of the things I enjoyed most in my entire life. It certainly influenced me to study mathematics. Unfortunately, the Saint Mary’s Math Contest no longer exists, and I wasn’t able to find another like it. In the spring of 2005, I attended the East Bay Community Foundation/California Math Council/MSRI Sharing Solutions: Promising Practices in Science & Math Education forum. I asked MSRI’s deputy director at, Hugo Rossi, whether he knew what happened to the Saint Mary’s Math Contest. He didn’t, but he emailed a note to some of his colleagues asking what they knew about the contest.
Joshua Zucker, a math teacher at Castilleja School in Palo Alto, responded to Hugo’s email because he had a book containing problems from the Saint Mary’s Contest, which he had won in his high school days at a math contest in Southern California. (I've included some Saint Mary's Contest problems at the end of this article.) Joshua had also come across files containing old fliers when he worked at Gunn High School in Palo Alto. He said he’d like to organize a festival at the middle- or high-school level if MSRI would provide some funding for prizes, mailings, and small honoraria for problem-writers.
Jim Sotiros, the MSRI development director [at the time], suggested that my husband David desJardins, also a mathematician, and I fund MSRI specifically to hire Joshua Zucker to resurrect the Saint Mary’s Math Contest. In February of 2007, we were satisfied with Josh’s proposal and decided to fund the festival.
Since the school year was well under way and there wasn’t enough time to create qualifying problem sets, we decided just to have a math day. We wanted to emphasize fun rather than competition, so we decided to call it a festival. There would be two dozen or so tables with math problems, puzzles, games, and activities, each with a facilitator to check solutions and guide students who needed or desired assistance.
Since the festival was meant to nurture the students’ interest in math, we let them work individually or in groups as they preferred. The problems and activities would be related to one another and get progressively more difficult—we even included research problems whose answers we didn’t know ourselves. We envisioned having so many problems that not even a mathematical genius could solve all of them during the festival, and hoped that each attendee would be able to find something rewarding at his or her level.
We wanted to name the festival for someone inspirational, and thought of Julia Robinson, a great mathematician renowned for solving, together with Yuri Matijasevich, Martin Davis, and Hillary Putman, Hilbert’s Tenth Problem. Her husband, Raphael Robinson, was a professor in the mathematics department at the University of California at Berkeley, but she was relegated to the low-level position of lecturer until the National Academy of Sciences named her—the first woman mathematician to be so honored—as a member. At that point the department made her a full professor. She served with distinction in that role for many years, and died in 1985. When we began to plan the festival, we were able to contact her sister, Constance Reid, who gave us permission to use Julia’s name. The festival is intended to honor her legacy and encourage more students to pursue mathematics.

Julia Robinson in May 1941. (Photo courtesy of Constance Reid)
Constance told us that Julia had often been annoyed when people referred to mathematics as math, so we were careful to call the event the Julia Robinson Mathematics Festival. David, my husband, emailed Peter Norvig, a co-worker from his days at Google, and asked if Google would host the first festival. Feeling that the event would encourage girls and minorities—groups underrepresented in the company’s workforce—to go further in mathematics, Google was willing to give it a try.
In March 2007 Joshua sent announcements for the festival to many junior high and high school math teachers in the San Francisco Bay Area. We were concerned that we might not get many students to sign up, but within a few weeks, the festival was oversubscribed. With more registrants than space, we asked Google for a tent to accommodate more students, which they provided.
The festival featured 30 tables with activities, puzzles, games, and problems. If a participant showed insight, creativity, perseverance, or solved a problem correctly, the facilitator at that table would give the student a raffle ticket. Participants could place their raffle tickets in one of three boxes. Winning tickets drawn from the first box would receive a math book; from the second, Google paraphernalia, e.g. water bottles, umbrellas, hats and jackets; winning tickets drawn from the third box would either get a tour of Google or a chance to shadow a Google engineer for half a day. All participants received a festival T-shirt and a yo-yo that lit up when it spun.
Response to the first festival was so enthusiastic that we hosted another the next year on May 4, 2008, at Pixar Animation Studios in Emeryville. Computer technology, computational physics and geometry are driving a digital revolution in film making, so senior scientist Tony DeRose, lead of Pixar’s Research Group, offered to have the company host the festival. Google hosted another festival the same year. In 2009, we had festivals at Pixar, Stanford University, and the University of California at Los Angeles. This year there were festivals in Arizona, California, North Carolina, Virginia, and Wyoming. Most of the festivals have been oversubscribed.
The initial format worked so well the first year that we have kept it. JRMF is a less intense festival than other contests, and places more emphasis on collaboration than competition: participants help each other.
My goal was to inspire, delight, and challenge children, as the Saint Mary’s Math Contest did for me. Thanks to Joshua Zucker, Jim Sotiros, David desJardins, and many facilitators, the Julia Robinson Mathematics Festival is a success.
I thank Mary Eisenhart for her assistance with writing this paper; I revised this paper incorporating the valuable comments and suggestions from my father, Nelson Blachman; from Julia’s sister, Constance Reid; and from Emily McCullough and Jessica Hansen, to all of whom I am grateful. Thanks to Joshua Zucker, the Director of the Julia Robinson Mathematics Festival, for providing the math problems in this paper.
Problems and Activities
The following problems are from Saint Mary’s College Mathematics Contest Problems: For Junior and Senior High School by Brother Alfred Brousseau, Palo Alto: Creative Publications, 1972.
77. By what rule based on the digits in a number is it possible to tell whether a number in base 7 is even?
92. Given the sequence 1, 2, 4, 5, 7, 8, 10, 11, 13, 14, ... where every third integer is missing, find the sum of the first hundred terms in the sequence.
98. A pyramid is formed in the following fashion: the first layer is made up of 169 equal cubes arranged in the form of a square; the second layer is symmetrically placed and has 11 cubes on a side; the third layer has 9 cubes on a side; etc. The final layer has but one cube. This whole structure is painted (but not the bottom). When it is taken apart, how many cubes have no faces, 1 face, 2 faces, 4 faces, 5 faces, 6 faces painted?
116. Cards are given numbers: 1 for ace, 2 for 2, ..., 11 for jack, 12 for queen and 13 for king. Let one player secretly count out three piles of cards as follows: Starting with any card, such as 7, put down cards counting 7, 8, 9, 10, 11, 12, 13. Turn the pile face down; do likewise for two other piles. Now turn two piles over so that the other player can see the starting cards. This player now counts out ten cards plus a number of cards equal to the sum of the numbers shown on the two piles. Prove that the number of cards remaining in the pack gives the number on the bottom of the unturned pile.
129. Show how to make six equilateral triangles with nine toothpicks of equal length, the sides of the triangles all being the length of one toothpick.
144. A company named TOPIC has an advertising display with the letters of its name “TOPIC”. Colors are to be used for each letter, but the colors may be repeated. On a certain day the colors might be red, green, green, blue, red. The company wishes to have a different color scheme for each of the 365 days of the year. What is the minimum number of colors that can be used for this purpose?
158. A computer is programmed to scan the digits of the successive integers 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 13, 14, 15, ... . To this point it has scanned 21 digits. It continues until it has scanned 6,000,000,000,000 digits. At what integer has it arrived?
177. Using five 5’s and the operations +, -, ×, ÷, 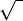 , and factorial (!), represent the numbers up to 30 inclusive by using five 5’s in each case.
, and factorial (!), represent the numbers up to 30 inclusive by using five 5’s in each case.
Sample Julia Robinson Mathematics Festival Activities
|
|
| Difficulty | ||||
|---|---|---|---|---|---|---|---|
Name | Topics | Years | 1 | 2 | 3 | 4 | 5 |
Area | 2007, 2008, 2009 | * | * | * |
|
| |
Bayes' theorem, probability, judgement | 2007 | * | * |
|
|
| |
Factorials, comparisons, divisibility, Pascal's triangle, calculus | 2008, 2009 | * | * | * | * |
| |
Area, Volume, Binary, optimization | 2008, 2009 | * | * | * | * |
| |
Counting, probability, ratio, lattice points | Demo | * | * | * | * |
| |
Counting, infinity | 2008 |
|
| * | * | * | |
Counting, recursion | 2008, 2009 | * | * | * | * | * | |
Symmetry, patterns, patience | 2009 | * | * | * |
|
| |
Coloring, counting, cutting | 2008 | * | * | * |
|
| |
Counting, patterns, geometry | 2007, 2008 | * | * | * |
|
| |
Graph theory, Euler's formula | 2007, 2008 | * | * | * |
|
| |
Patterns, lines, planes, space | 2009 | * | * | * | * |
| |
Counting, factorial, Pascal's Triangle, statistics | 2007 | * | * | * | * |
| |
Subtraction, patterns, parity | 2007, 2009 | * | * | * | * | * | |
Addition, linear equations, integers | 2007 | * | * | * | * |
| |
Geometry, area, cutting, 3D | 2009 |
| * | * | * |
| |
Tiling, recursion, counting, 3D | 2009 |
| * | * | * |
| |
Game theory | 2007 | * | * | * | * |
| |
Fractions, primes, common factors, remainders | 2007 | * | * | * | * |
| |
Probability | 2009 |
| * | * | * | * | |
Fibonacci Flips and Probability Puzzles(2007 version) | Probability, counting, recursion, Markov | 2007, |
| * | * | * |
|
Recursion, patterns, fractals, turing machines | 2008, 2009 |
| * | * | * |
| |
Fractals, hands-on, dimension, geometry | 2009 | * | * | * |
|
| |
Algebra, composing functions, maximization | 2008, 2009 |
| * | * |
|
| |
Recursion, patterns, computer science | 2009 | * | * | * | * |
| |
Recursion, combinatorics | 2009 |
| * | * | * | * | |
Making Infinity Finite | Recursion, series, limits, probability, Markov chains | 2008, 2009 |
|
| * | * |
|
Kakuro Counting | Counting, partitions, compositions | 2007, 2008 | * | * | * | * | * |
Factors, primes, inverses | 2007 | * | * | * | * | * | |
Area, fractions, infinite series | 2007, 2008 | * | * | * |
|
| |
MIMPSY: Mathematically Interesting Mechanical Puzzles Suitable for Youth. | Geometry, parity, volume, logic | 2007, 2008, 2009,2010 | * | * | * | * |
|
Multiplication Table | Multiplication | 2007, 2008, 2009 | * | * | * |
|
|
Symmetry, game theory | 2009 |
| * | * | * |
| |
Primes, perfect squares, addition, arrangements | 2009 | * | * | * |
|
| |
Area, lattice polygons, pattern | 2007 | * | * |
|
|
| |
Counting, sets | 2007 | * | * | * |
|
| |
Logic | 2007 |
| * | * | * |
| |
Probability, expected value, logic, patterns | 2009 | * | * | * | * |
| |
